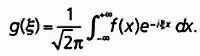Жуан Гомес - Мир математики. т.4. Когда прямые искривляются. Неевклидовы геометрии

Преобразование Фурье изучается в разделе математики, называемом гармоническим анализом. Этот математический оператор используется, чтобы разложить сигнал на составляющие разной частоты. Математически это очень сложно. Этот оператор задается для функций f и g комплексного переменного следующим образом:

* * *

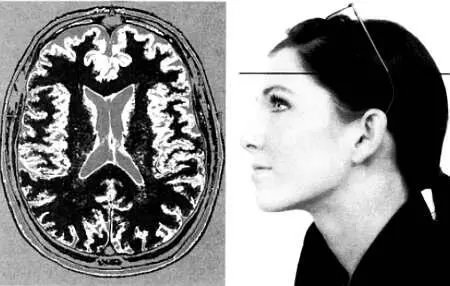
Магнитный резонанс позволяет изображать срезы внутренних органов. Изображение слева — горизонтальный срез головного мозга в месте, указанном стрелкой на фотографии справа.

И наконец, изображение представляется в виде точек, яркость которых пропорциональна силе магнитно-резонансного сигнала в соответствии с содержанием вокселей в изучаемом объекте. Эта информация отображается и распечатывается в виде изображения с числовыми значениями, так что медицинские специалисты могут визуально интерпретировать его и точно диагностировать состояние пациента.

Отправка и получение фотографий по электронной почте, фотографирование цифровой камерой, сканирование изображений — все это теперь часть нашей повседневной жизни. Благодаря многочисленным программам для обработки изображений и плоским экранам во всех языках появились новые регулярно и повсеместно используемые слова. Например, пиксель, уже упомянутый выше, а также растровые и векторные изображения с поразительной легкостью из специализированных терминов стали общеупотребительными словами.

Как и новые термины, приходящие из других языков, понятие «растровое изображение» может принимать различные обличья: битовая матрица, матричное изображение или пиксельное изображение. Это файл, представленный в виде матрицы, таблицы пикселей или цветных точек, называемый растром, который можно просматривать на экране компьютера или в распечатанном виде. Слово растр происходит от латинского rastrum , означающего «грабли», и radere — «скрести».

Векторное изображение представляет собой цифровой рисунок, образованный отдельными геометрическими объектами, то есть линиями, многоугольниками, дугами и т. д. Векторные изображения, в отличие от растровых, могут быть увеличены до бесконечности без потери их очертаний, и поэтому они используются в графическом дизайне или в компьютерных играх для создания виртуальной реальности.

У растровых изображений графический контур не сохраняется по мере увеличения размера.

* * *

ПИКСЕЛЬ

Слово «пиксель» является неологизмом. Оно означает «элемент изображения» и служит минимальной единицей цифрового изображения, которое можно просматривать на различных устройствах, как правило, подключенных к компьютеру, например, на мониторе. Размер пикселя не одинаков, он меняется в зависимости от устройства, используемого для просмотра изображения. Большинство компьютерных мониторов имеют 72 пикселя на дюйм экрана.

Изображение размером 16 на 16 пикселей.

* * *

Следующие фотографии являются увеличением исходного изображения (100 %). Буква А слева — векторное изображение, а буква А справа — растровое изображение.

Многократное увеличение выявляет различие между этими двумя типами. При увеличении векторная буква А (слева) сохраняет качество изображения, в то время как растровая буква А (справа) постепенно превращается в размытую мозаику пикселей. Если мы увеличим изображение достаточно сильно, например, на экране компьютера, мы сможем разглядеть пиксели, из которых оно состоит. Изображение является прямоугольной матрицей пикселей, каждый из которых представляет собой крошечную часть общей картины. Они похожи на маленькие квадраты или прямоугольники и могут быть цветными, черными, белыми или серыми.

Чтобы преобразовать цифровую информацию пикселя в цвет, мы должны знать глубину и яркость цвета, закодированного в пикселе, а также используемую цветовую систему. Например, RGB-система ( Red Green Blue — красный, зеленый, синий) позволяет создавать цвета из трех основных цветов: красного, зеленого и синего. Их сочетание определяет, какой цвет мы видим. Большинство компьютерных периферийных устройств — мониторы, сканеры и т. д. — используют систему RGB.