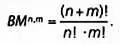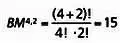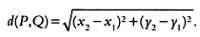
Мы могли бы попробовать различные другие маршруты, чтобы найти наименьшее расстояние. Вариантов множество. Мы можем двигаться по вертикали и по горизонтали, поворачивая на первую улицу, а затем на вторую, или сделать поворот через две улицы и так далее. Однако общее расстояние всегда будет 6 единиц.
На следующем рисунке изображены различные маршруты между точками А и В . Всего имеется 15 возможностей.
Выходит, что фактический маршрут вовсе не является прямой линией. Здесь появляется другое понятие расстояния, которое называется расстоянием такси . Это понятие нелинейного расстояния лежит в основе геометрии такси .
* * *
ВОЗМОЖНЫЕ МАРШРУТЫ
Формула, выражающая количество всех возможных маршрутов для n вертикальных и m горизонтальных движений, выглядит следующим образом:
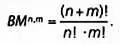
Здесь n! означает факториал числа n, который равен n ·( n -1)·( n -2)·…·2·1. Например, 5! = 5–4 — 3–2 — 1 = 120. В нашем примере формула записывается так:
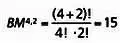
возможных маршрутов.
* * *
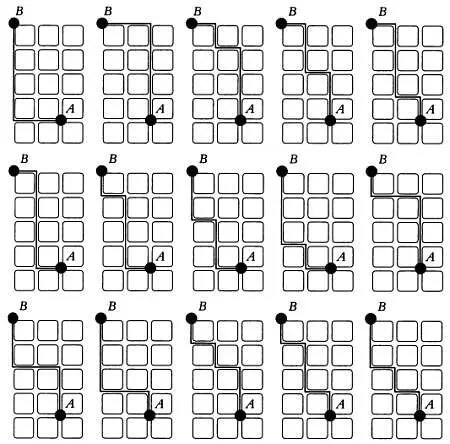
Расстояние такси
Расстояние, которое изучается в школе, является евклидовым расстоянием. Оно находится по теореме Пифагора, поэтому расстояние между двумя точками Р и Q с координатами Р = ( x 1, y 1 ) и Q = ( x 2, у 2 ) выражается следующей формулой:
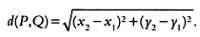
В отличие от евклидова расстояния, минимальное расстояние в городе с прямоугольной сеткой улиц считается как d T ( P, Q ) = | x 2— x 1 | + | y 2— y 1 |
* * *
АБСОЛЮТНОЕ ЗНАЧЕНИЕ
Выражение | А | означает «абсолютное значение числа А», которое получается путем игнорирования знака числа. Если число А положительно, то | А | = А , а если число А отрицательно, то | А | = — А , например, |-5| = 5.
* * *
Это альтернативное расстояние называется манхэттенским расстоянием , или расстоянием Минковского, в честь немецкого математика Германа Минковского.
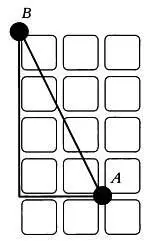
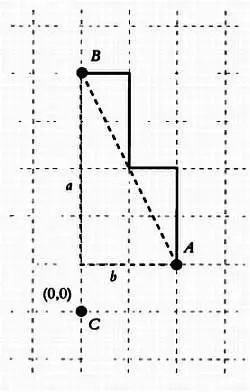
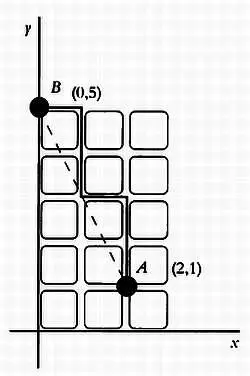
На более популярном языке это расстояние называют также расстоянием такси . На рисунке ниже пунктирная линия отмечает евклидово расстояние, а сумма длин вертикальных и горизонтальных отрезков соответствует расстоянию такси.
Если точка С является началом координат, то точка А имеет координаты (2, 1), а точка В — координаты (0, 5). Таким образом, евклидово расстояние составляет 4,47 единиц, а расстояние такси — 6 единиц. Обратите внимание, что положение начала координат не влияет на результат при расчете расстояний.
В математике метрикой или расстоянием между двумя точками А и В называется такое соотношение, которое удовлетворяет условиям положительности, симметрии и неравенства треугольника. А именно,
1) δ( A, В ) >= 0, и из δ( A, В ) = 0 следует, что А = В ;
2) δ( A, В ) = δ( В, A );
3) δ( А, В ) =< δ( А, С ) + δ( С, В ).
Евклидово расстояние d( A, В ) и расстояние такси d t( A, В ) — два примера расстояний, которые удовлетворяют указанным выше условиям. В общем случае d( A, В ) =< d T( A, В ).
* * *
ГЕРМАН МИНКОВСКИЙ(1864–1909)
Немецкий математик Герман Минковский разработал геометрическую теорию чисел — геометрический метод решения задач из теории чисел. В 1907 г. он понял, что специальная теория относительности Эйнштейна может быть лучше выражена в терминах неевклидовой геометрии четырехмерного пространства. Это пространство с тех пор называется пространством Минковского. В нем время и пространство являются взаимосвязанными измерениями и образуют четырехмерное пространство, так называемое пространство-время. Именно таким подходом позже воспользовался Эйнштейн при работе над общей теорией относительности.
Читать дальше