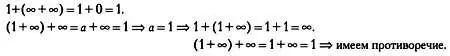Необычная алгебра
Порой реклама автомобилей представляет собой настоящий полет творческой мысли. В последние годы все чаще основной упор делается на технологии, геометрию и математику. Это особенно заметно в рекламе дорогих автомобилей.
В одной рекламной кампании, запущенной несколько лет назад, был показан автомобиль, отражавшийся в идеально зеркальной поверхности пола. В результате казалось, что автомобиль словно парит над зеркалом. Над изображением автомобиля можно было прочесть формулу и слоган:
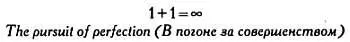
Имеет ли какое-то отношение равенство 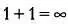 к стремлению к совершенству?
к стремлению к совершенству?
Сначала может показаться, что приравнять к бесконечности сумму двух конечных чисел, какими являются единицы, нельзя, поскольку неожиданно получается:
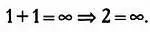
Быть может, это равенство имеет какой-то смысл? Пусть в повседневной трактовке бесконечности и в привычной трактовке суммы чисел это не так, однако существуют и другие трактовки, в которых это равенство может быть абсолютно верным.
Будем рассматривать не множество натуральных чисел в целом, а множество X , содержащее всего три элемента:
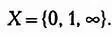
Сопоставим элемент 0 с нулем, элемент 1 — с произвольной конечной величиной, элемент ©о — с некоторой величиной, которая не является ни нулевой, ни конечной. С учетом вышесказанного логично предполагать, что
Ничто + что-то = что-то.
Конечное + конечное = конечное.
Бесконечность + что-то = бесконечность.
Поэтому сумма 1 + 1 должна быть не бесконечной, а конечной, а операция сложения на множестве X должна описываться следующей таблицей:
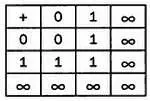
Эта операция сложения обладает привычными нам свойствами. Так, она коммутативна (описывающая ее таблица симметрична относительно диагонали), содержит нейтральный элемент (ноль), который при сложении с любым другим элементом оставляет его неизменным, кроме того, эта операция обладает ассоциативностью (порядок сложения трех элементов не влияет на итоговый результат). Сохранятся ли эти свойства, если мы заменим равенство 1 + 1 = 1 на , как указано в рекламном слогане? Иными словами,
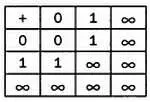
В этом случае таблица по-прежнему симметрична относительно диагонали. Ноль по-прежнему является нейтральным элементом. Свойство ассоциативности также сохраняется.
Однако не выполняется одно из ожидаемых свойств — ни для 1, ни для 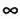 нет противоположного элемента. Не существует элемента, который в сумме с 1 давал бы 0, и не существует элемента, который в сумме с давал бы 0. Чтобы исправить это, необходимо, чтобы в каждой строке или в каждом столбце таблицы имелся минимум один 0. Очевидно, что если заполнить таблицу нулями, проблема будет решена, однако подобное решение нас не устраивает.
нет противоположного элемента. Не существует элемента, который в сумме с 1 давал бы 0, и не существует элемента, который в сумме с давал бы 0. Чтобы исправить это, необходимо, чтобы в каждой строке или в каждом столбце таблицы имелся минимум один 0. Очевидно, что если заполнить таблицу нулями, проблема будет решена, однако подобное решение нас не устраивает.
Цифры в первой строке и в первом столбце таблицы неоспоримы, так как при сложении нуля с любой величиной результатом всегда является эта величина. Если мы определим , новая таблица примет вид:
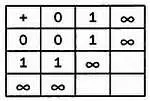
Чтобы для операции сложения были определены противоположные элементы, 0 должен встречаться в каждой строке и в каждом столбце. Если мы хотим, чтобы эта операция обладала коммутативностью, таблица должна быть симметричной относительно диагонали. Обеспечить это можно всего несколькими способами:
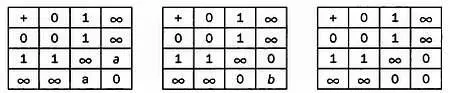
Не существует значения а такого, чтобы операция сложения, определенная в первой таблице, обладала бы ассоциативностью:
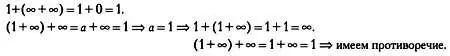
Третья таблица также не подходит:
Читать дальше

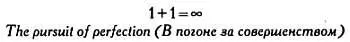
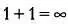 к стремлению к совершенству?
к стремлению к совершенству?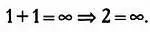
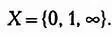


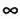 нет противоположного элемента. Не существует элемента, который в сумме с 1 давал бы 0, и не существует элемента, который в сумме с давал бы 0. Чтобы исправить это, необходимо, чтобы в каждой строке или в каждом столбце таблицы имелся минимум один 0. Очевидно, что если заполнить таблицу нулями, проблема будет решена, однако подобное решение нас не устраивает.
нет противоположного элемента. Не существует элемента, который в сумме с 1 давал бы 0, и не существует элемента, который в сумме с давал бы 0. Чтобы исправить это, необходимо, чтобы в каждой строке или в каждом столбце таблицы имелся минимум один 0. Очевидно, что если заполнить таблицу нулями, проблема будет решена, однако подобное решение нас не устраивает.