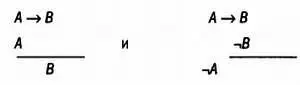Хавьер Фресан - Том. 22. Сон разума. Математическая логика и ее парадоксы

Икар — человек, следовательно, он может летать» — корректен, в то время как высказывание: «Если идет дождь, земля мокрая. Земля мокрая, следовательно, прошел дождь» корректным не является. Хотя высказывание о мокрой земле после дождя выглядит разумным, а высказывание о летающих людях — совершенно абсурдным, первое высказывание корректно, а во втором перепутаны причина и следствие. Действительно, после дождя земля мокрая, однако если земля мокрая, это необязательно связано с дождем: например, по улице просто могла пройти поливальная машина. Также существует modus tollens (от лат. modus tollendo tollens — «путь исключения исключений»), который гласит, что из утверждения «Если А , то В » при ложном В выводится ложность А , как в высказывании «Если что-то неизвестно, об этом лучше промолчать. Если я говорю, то я знаю, о чем говорю».

* * *

ОБОЗНАЧЕНИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Структуру modus ponens и modus tollens удобнее запомнить, если записать их в виде схем, в которых посылки и заключение разделены линией. Если мы обозначим через ¬Аи ¬Вотрицания Аи В, то есть утверждения, противоположные им по смыслу, то modus ponens и modus tollens будут описываться следующими схемами:

* * *

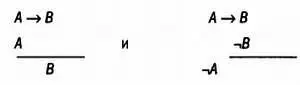
В общем случае правило вывода верно, когда его результат является истинным вне зависимости от толкования посылок. Так, высказывание «Если Р и Q , то R » корректно вне зависимости от значений Р, Q и R : всякий раз, когда Р и Q одновременно будут истинными, R также будет истинным. И вновь речь идет о формальном критерии, который подразумевает, например, что высказывание «Если ноль отличается от единицы и если единица равна нулю, то вы мой отец» является корректным. Так как ни в одном из возможных миров ноль не может отличаться от единицы и одновременно быть равным ей, исходные посылки никогда не будут верными. Это понимали уже схоластики, которые сформулировали выражение ех contradictione sequitur quodlibet , то есть «из противоречия следует все что угодно».

* * *

MODUS TОLLENS И ФАЛЬСИФИЦИРУЕМОСТЬ

Согласно философу Карлу Попперу(1902–1994), modus tollens — это единственное корректное правило вывода в естественных науках. Когда мы пытаемся объяснить какое-то явление, то научный метод, который Поппер назвал гипотетико-дедуктивным, заключается в том, чтобы выдвинуть гипотезу и провести эксперимент, который позволит опровергнуть ее. Если из гипотезы Нследует наблюдаемое следствие 0, которое неизменно повторяется в лабораторных условиях, то Нстановится научным законом. Однако если мы не можем поочередно проверить все возможные ситуации, в которых применима наша гипотеза, то мы никогда не сможем быть уверенными в ее истинности. Чтобы быть уверенными в том, что все лебеди — белые, нужно исследовать все уголки планеты, однако достаточно увидеть всего одного черного лебедя, как это произошло с первыми поселенцами в Австралии, чтобы опровергнуть гипотезу. Этот принцип известен под названием принципа фальсифицируемости и является не чем иным, как modus tollens : «Если гипотеза Нверна, то из нее следует следствие 0. Так как мы наблюдаем противоположное 0, то гипотеза Нложна».

Философ Карл Попперв 1980-е годы.

* * *

Теперь, когда мы знаем, что такое аксиомы и правила вывода, мы можем дать точные определения понятиям «теория», «доказательство» и «теорема», которые на предыдущих страницах более или менее соответствовали привычным представлениям. Доказательство — это процесс, позволяющий получить новые результаты путем применения правил вывода к аксиомам. На практике доказательство представляет собой конечную последовательность утверждений, или высказываний, первое из которых обязательно должно быть аксиомой (в математике нет «чистых листов»!), а каждое из последующих может быть либо аксиомой, либо выводиться из предшествующих высказываний с помощью правил вывода. Последнее высказывание доказательства называется теоремой. Теория — это множество аксиом, правил вывода и всех теорем, которые можно доказать с помощью этих правил на основе аксиом. В некоторых случаях вместо «теория» мы будем говорить «система аксиом».