Эдуардо Арройо - Том 42. Путешествие от частицы до Вселенной. Математика газовой динамики

1. Посчитай число символов во фразе и сохрани результат в х .

2. Вычисли остаток деления х на два и сохрани результат в r .

3. Если r равен нулю, напиши на экране: «Число символов четное».

4. Если r не равен нулю, напиши на экране: «Число символов нечетное».

* * *

ГРЕГОРИ ХАЙТИН

Грегори Хайтин, родившийся в 1947 году, — аргентинско-американский программист и математик. Еще будучи подростком, он вывел алгоритмическую теорию информации и свою собственную версию теоремы Гёделя о неполноте, где показал, что количество недоказуемых теорем в математике намного больше, чем было принято считать. Сейчас Хайтин занимается метабиологией — математическим подходом к биологии, который изучает случайное развитие компьютерных программ для понимания биологической эволюции и возникновение творчества в строгой математической форме.

* * *

Согласно алгоритмической теории информации, информация, содержащаяся в цепочке символов, задана длиной самой короткой программы, которая ее порождает. Возьмем цепочку:

Существует программа, порождающая ее с помощью очень короткого кода.

1. Напиши единицу.

2. Вернись к началу программы.

В этой цепочке содержится очень мало информации.

Важно, что количество информации зависит от используемого языка программирования. Так, программа на языке Java и программа на языке С имеют разное количество строк, даже если обе делают одно и то же. Чтобы преодолеть эту проблему, воспользуемся понятием универсального языка программирования: язык программирования универсален, если его можно использовать для написания любой программы, которую можно написать на любом другом языке. Все существующие сегодня языки программирования универсальны, в том смысле что можно создать программу на языке Java , которая понимала бы программы, написанные на С , и наоборот. Хотя содержание информации в этих программах будет разным, эти отличия относительно небольшие и зависеть они будут не от количества строк кода, а от разницы между двумя языками программирования. А эта разница всегда постоянна.

Применим алгоритмическое определение информации к вычислению знаков числа π . Вспомним, что, согласно Шеннону, количество информации, содержащейся в числе π , бесконечно. Однако существует простая формула, которая позволяет довольно точно вычислить знаки этого числа. Выглядит она следующим образом:

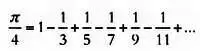
На основании этой формулы можно создать очень короткую программу. И это означает, что в соответствии с алгоритмической теорией π не содержит бесконечного количества информации.

Как видите, в этом конкретном случае алгоритмический подход несколько отличается от предложенного Шенноном, но в большинстве других случаев они согласуются. Например, для передачи случайной последовательности нулей и единиц самой короткой программе необходимо столько же бит, сколько цифр содержится в цепочке.

Возникает вопрос: существует ли число, содержащее бесконечное количество информации по определению Колмогорова и Хайтина (подобное π в определении Шеннона)? Да, такое число существует, и это одно из самых удивительных чисел в истории математики — число омега, известное также как постоянная Хайтина . Ее свойство заключается в том, что эта постоянная не может порождаться кодом, содержащим меньше битов, чем она сама. Это означает, что все биты числа омега полностью случайны.

Для того чтобы понять, что такое постоянная Хайтина, поговорим о проблеме остановки, которая заключается в том, чтобы определить, остановится ли какая-либо программа. Так, мы знаем, что программа, вычисляющая 2 + 2, остановится, как только будет найдена требуемая сумма. Но точно так же программа, вычисляющая все простые числа, не остановится никогда. Можно доказать, что способа решить проблему остановки для любой программы не существует: мы можем узнать, остановится ли какая-то конкретная программа, но не можем сделать этого для любого алгоритма.

Например, представим себе программу, которой даны инструкции остановиться при нахождении четного числа, которое не может быть выражено как сумма двух простых. Программа остановится, если существует четное число с такими характеристиками, и никогда не остановится в противном случае. Ни один математик до сих пор не смог найти ответ на эту проблему, связанную с доказательством гипотезы Гольдбаха, в которой утверждается, что любое четное число может быть выражено как сумма двух простых чисел. Сегодня кажется, что гипотеза верна — по крайней мере, уже полученные результаты вычислений вполне ей соответствуют, но не доказано, что эта тенденция сохранится до бесконечности.