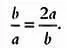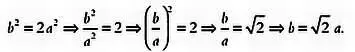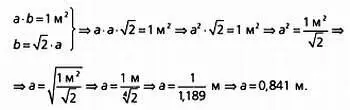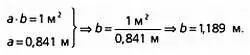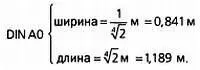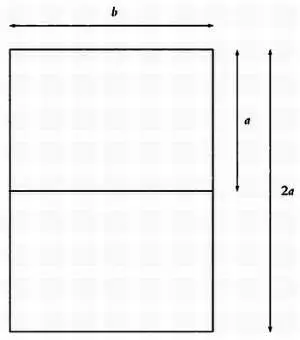
Формат листа бумаги, соотношение сторон которого при складывании пополам остается неизменным.
Как найти искомое соотношение? Рассмотрим прямоугольный лист бумаги со сторонами а и b соответственно. Лист бумаги большего формата должен иметь стороны 2 а и b . Чтобы соотношение длин его сторон было прежним, должно выполняться условие:
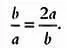
Следовательно:
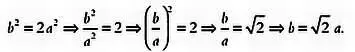
Иными словами, соотношение длины большей стороны к меньшей должно равняться √2. Если мы разрежем пополам лист бумаги, удовлетворяющий этому условию, то указанное соотношение сторон будет выполняться и для двух полученных листов.
Зная размеры листа формата А0, несложно определить размеры листа следующего формата (А1): достаточно разделить его большую сторону пополам и принять длину большей стороны листа А1 равной длине меньшей стороны листа А0. Если мы выполним аналогичные действия для листа А1, точнее, разделим его большую сторону пополам и оставим меньшую сторону неизменной, то получим лист формата А2 и так далее, как показано на следующем рисунке.
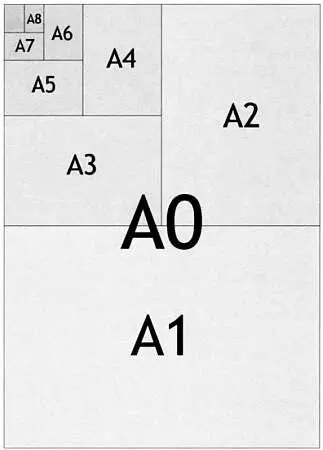
Размеры листов бумаги формата DIN.
* * *
РАСЧЕТ РАЗМЕРОВ ЛИСТА ФОРМАТА А0
Прямоугольник со сторонами аи bдолжен иметь площадь 1 м 2, при этом длины его сторон должны удовлетворять соотношению b= √2· а:
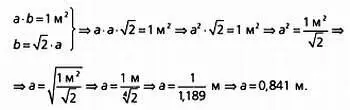
Зная а, мы с легкостью вычислим b:
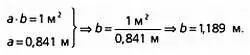
Таким образом, лист бумаги формата DIN А0 имеет следующие размеры:
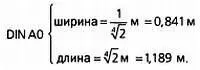
* * *
Прямые и косвенные измерения
Измерения могут быть прямыми, например измерение температуры термометром, и косвенными — в этом случае для получения результата требуется несколько измерений. Если мы проводим измерения с помощью специального измерительного инструмента, то речь идет о прямых измерениях. В таких случаях мы получаем результат, сравнивая измеряемую величину с другой величиной, имеющей ту же физическую природу. Это происходит, к примеру, при сравнении длины объекта с длиной размеченного эталона.
Методы измерений — это приемы, используемые для измерения величины: подсчет, оценка, использование формул или применение измерительных инструментов.
Большинство людей ассоциируют с измерением именно применение инструментов — линеек, рулеток, мерных сосудов, термометров, часов, хронометров и так далее.
Иногда прямое измерение невозможно: во-первых, существуют величины, которые нельзя измерить путем сравнения с эталоном той же природы, во-вторых, рассматриваемая величина может быть слишком мала или слишком велика, и у нас не найдется подходящего инструмента для ее измерения. В таких ситуациях следует прибегнуть к косвенному измерению: провести измерение с помощью какой-то другой величины и вычислить искомое значение на ее основе.
При использовании формул и отношений для определения новых мер особую роль играют треугольники, что подтверждает и история математики. Всем известна теорема Пифагора со множеством доказательств, найденных разными культурами в разное время и в разных регионах: в Египте, Греции, Африке, Китае, Индии и Европе. Также особую роль треугольников подчеркивают отношение подобия треугольников и теорема Фалеса, которые позволяют проводить косвенные измерения. Кроме того, треугольник является основным элементом тригонометрии. Эта математическая дисциплина, на протяжении многих веков связанная с астрономией, описывает основы расчетов, необходимых для астрономических измерений. Тригонометрия лежит и в основе триангуляции — метода измерения дуг земных меридианов (мы расскажем об этом в следующих главах).
Рассмотрим косвенное измерение на примере подобия фигур, в частности прямоугольных треугольников. Допустим, что мы хотим измерить высоту очень высокой башни или здания. По какой-то причине мы не можем подняться на его вершину, чтобы произвести прямые измерения, опустив, к примеру, веревку или рулетку до самой земли. Но мы можем определить высоту башни с помощью простого косвенного метода.
Читать дальше