Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

* * *

«Живая» гистограмма. Каждый человек стоит в колонне, соответствующей его росту.

(источник: Эдвард Тафти. Наглядное отображение количественной информации. Цитируется работа Brian L. Joiner«Living Histograms», опубликованная в 1975 году в журнале International Statistical Review.)

Есть и еще одна причина, по которой нормальное распределение играет столь значительную роль. Очень часто в статистических исследованиях основное внимание уделяется средним значениям: анализируется средняя урожайность в зависимости от использованного удобрения, среднее значение выборки сравнивается с предполагаемым средним значением генеральной совокупности и так далее. Средние значения варьируются в зависимости от того, каким образом была взята выборка. Их вариацию на практике можно описать с помощью закона нормального распределения, даже если исходные данные генеральной совокупности не подчиняются этому закону. Например, число очков, выпадающее при броске игральной кости, совершенно не подчиняется закону нормального распределения. Это дискретное распределение с шестью возможными значениями: 1, 2, 3, 4, 5 и 6. Вероятность выпадения каждого из них одинакова. Если мы бросаем два кубика и анализируем среднее число выпавших очков, то частота выпадения различных средних значений уже не будет одинаковой.

Наиболее вероятно, что среднее значение будет равно 3,5. Если мы бросаем четыре кубика, то столбиковая диаграмма, представляющая вероятность возможного среднего числа выпавших очков, будет напоминать колокол Гаусса. Если мы будем бросать 10 кубиков, что равносильно взятию выборки величиной 10, то на диаграмме будет очевидно вырисовываться колокол Гаусса. Таким образом, распределение средних значений подчиняется нормальному закону.

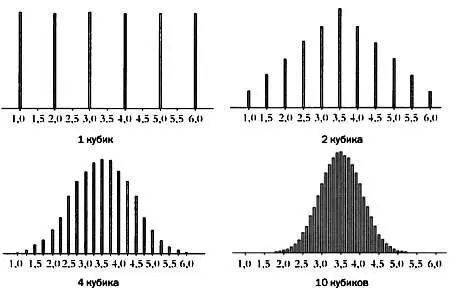
Распределение средних значений стремится к нормальному, хотя исходные значения не подчиняются нормальному закону.

Тем не менее хотя этот закон распределения встречается очень часто, название «нормальный» — не самое удачное: можно подумать, что остальные чем-то необычны. Однако это название используется повсеместно, при этом некоторые предпочитают назвать его гауссовым распределением.

Если исходные данные по своей природе подчиняются нормальному закону (это также можно проверить графически или с помощью тестов), то их распределение полностью описывается всего двумя величинами: средним арифметическим, которое определяет центр колокола Гаусса, и среднеквадратическим отклонением, которое определяет форму колокола.

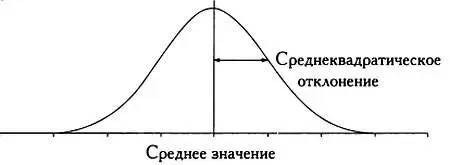
Среднее значение и среднеквадратическое отклонение — две величины, характеризующие нормальное распределение.

Если вес мешков с сахаром подчиняется нормальному закону, среднее значение равно 1000 г, среднеквадратическое отклонение — 5 г, то можно рассчитать, сколько мешков будут иметь вес свыше 1010 г, сколько — от 995 до 1010 г или менее 995 г. До недавнего времени для этого требовалось выполнять расчеты и сверяться со специальными таблицами (которые до сих пор включаются в некоторые учебники по статистике), но сегодня все расчеты можно выполнить автоматически с помощью электронных таблиц Excel . Например, вероятность того, что мешок сахара весит меньше 995 г, равна

Заметим, что приблизительно 16 % мешков имеют вес менее 995 г, но о весе конкретного мешка ничего определенного сказать нельзя. По этой же причине можно говорить об ожидаемой продолжительности жизни населения, но не о конкретной дате смерти отдельного человека.

Также существуют правила, основанные на том, что вне зависимости от среднего значения ( μ , читается «мю») и среднеквадратического отклонения ( σ , читается «сигма») 68 % значений будут лежать в интервале μ ± σ , 95 % — в интервале μ ± 2 σ , 99,7 % — в интервале μ ± 3 σ . Так, в прошлом примере среднее значение μ = 1000, среднеквадратическое отклонение σ = 5. В интервале 995—1005 будет лежать 68 % результатов. Следовательно, в этот интервал не попадает 32 % значений, по 16 % с каждой стороны. Это означает, что 16 % мешков будут иметь вес меньше 995 г.