Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

Рассмотрим конкретный пример. Представим сферический треугольник, образованный дугой меридиана, заключенной между Северным полюсом и экватором, и другой, похожей, дугой, отстоящей на угол π /2 (90°) от первой, как

Сферический треугольник, три угла которого равны 90°, следовательно, их сумма равна 270°.

Сумма углов этого сферического треугольника будет равна 3 π /2 (270°), а не π (180°), как мы ожидали. Следовательно, не существует проекций сферы на плоскость, которые сохраняли бы величины углов и геодезические линии одновременно. Из этого утверждения следует: не существует изометрических проекций сферы на плоскость, то есть

ИДЕАЛЬНОЙ КАРТЫ НЕ СУЩЕСТВУЕТ.

Более того, это утверждение касается не только всей сферы, но и любого ее участка. Локальную изометрию сферы на плоскости построить невозможно, следовательно, точную карту даже малой части земной поверхности построить также нельзя.

Чтобы доказать это, рассмотрим сумму углов произвольного сферического треугольника. Ее значение находится на интервале между π и 3 π (не включая границы). Так как каждый сферический угол меньше π , очевидно, что сумма трех углов будет меньше 3 π . Мы можем неограниченно приближаться к этому значению: достаточно рассмотреть треугольник, две вершины которого лежат на экваторе, а третья находится вблизи экватора так, что сферический треугольник покрывает почти все полушарие. Можно рассмотреть еще один предельный случай, когда две вершины треугольника лежат на экваторе, а третья совпадает с Северным полюсом так, что дуги меридианов будут образовывать сколь угодно малый угол. Сумма углов такого треугольника будет близка к π . Можно доказать, что для любого сферического треугольника выполняется равенство:

Площадь сферического треугольника = R 2 (сумма углов треугольника — π),

где R — радиус сферы. Так как сумма углов сферического треугольника произвольной формы и размера всегда больше π , не существует проекций участков сферы на плоскость, в которых сохранялись бы углы и геодезические линии. Следовательно, локальные изометрии также не существуют. Ожидания, которые мы возлагали на построение равновеликой конформной проекции, оказались напрасными.

Хотя в разные годы картографы неизменно терпели неудачу в попытках построить идеальную карту Земли, они не могли доказать, что эта задача не имеет решения. Доказательство принадлежит швейцарскому математику Леонарду Эйлеру, который изложил приведенные выше рассуждения в работе «О представлении сферической поверхности на плоскости«( De repraesentatione superficiei sphaericae super piano ), представленной в Петербургской академии наук в 1775 году и опубликованной в 1778 году в «Журнале Императорской Санкт-Петербургской академии наук».

* * *

ФОРМУЛА СУММЫ УГЛОВ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА

Пусть дана сфера радиуса R. Ее часть, заключенная между двумя большими кругами (сферический двуугольник), которые пересекаются под углом αрадиан, имеет площадь, равную площади поверхности сферы, взятой α/2 πраз, то есть

( α/2 π)·(4 πR 2).

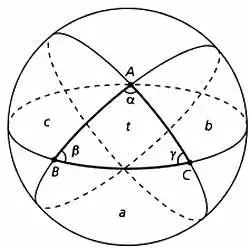
Обозначим вершины сферического треугольника через А, В, С, углы — через α, β и γ. Если мы рассмотрим большие круги, на которых лежат стороны АВи АС, по приведенной выше формуле получим:

t+ a= 2 αR 2

Аналогично имеем:

t+ b= 2 βR 2 и t+ c= 2 γR 2

Сложив эти три равенства, имеем:

3 t+ a + b+ c= 2 R 2( α+ β+ γ).

Получается, что t+ а+ Ь+ сравно площади поверхности полусферы (заметим, что для каждой вершины, например А, существуют два равных двуугольника с углами α; каждый из них состоит из двух областей площадью tи а). Как следствие,

2 t+ 2 πR 2= 2 R 2( α+ β+ γ).

Упростив равенство, получим

t = R 2( α+ β+ γ— π).