Хоакин Наварро - Том 31. Тайная жизнь чисел. Любопытные разделы математики

R 1031= (10 1031- 9)/9

На 2010 год это число было наибольшим из известных чисел Смита. Самым примечательным в этом классе является «число зверя» 666, упоминаемое в Откровении Иоанна Богослова:

С другой стороны,

6 + 6 + 6 = 18.

666 = 2·3·3·37;

2 + 3 + 3 + 3 + 7 = 18.

Трепещите, каббалисты и приспешники темных сил! Жаль, что числа Смита имеют столь прозаическое название и обязаны своим появлением на свет телефонному номеру.

Американский физик и математик венгерского происхождения Джон фон Нейман(1903–1957) благодаря некоторым чертам своего характера также стал героем множества анекдотов. В одном из самых популярных рассказывается о его впечатляющих способностях к вычислениям и любопытной привычке действовать не так, как простые смертные. Задача о двух поездах и мухе стала уже классической, и звучит она так: предположим, что два поезда, А и В , отправляются навстречу друг другу из точек и В соответственно. Допустим, что расстояние между A и В равно 100 км, скорость поездов — 50 км/ч. В момент отправления муха, сидевшая на локомотиве поезда А , летит в точку В со скоростью 75 км/ч. Она летит быстрее, чем движется поезд А , и в конце концов встречается с поездом В . Достигнув поезда В , она сразу же поворачивает обратно и летит в сторону А . Когда она достигает поезда А , она вновь поворачивает обратно и летит в сторону поезда В , и так далее. Полет мухи закончится, когда оба поезда встретятся. Какое расстояние к этому времени пролетит муха? После трудоемких вычислений студент-отличник показал бы, что длина пути равна сумме следующей бесконечной геометрической прогрессии:

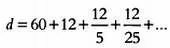
Знаменатель прогрессии равен 1/5, а ее сумма равна d = 75 км.

Проницательный неспециалист получит тот же результат, рассуждая следующим образом: поездам A и В встретятся в середине пути, на отметке в 50 км, время в пути составит один час. Следовательно, длительность полета мухи также равна одному часу, а поскольку скорость мухи равна 75 км/ч, то муха в сумме пролетит 75 км. Это решение элементарно, однако подойти к задаче подобным образом способны не все.

Когда один из коллег фон Неймана предложил ему эту задачу для развлечения, ученый незамедлительно дал ответ: «75 км». Коллега был несколько разочарован: «Ну вот, а я надеялся застать тебя врасплох. Ты очень умный, а вот большинство решает эту задачу с помощью суммы ряда». Фон Нейман с удивлением ответил: «А что я, по-твоему, сделал?» Гений среди гениев ни на секунду не задумался о другом решении. Он всего лишь вывел нужный ряд и мгновенно вычислил его сумму. Просто и быстро — если, конечно, вы — фон Нейман.

Некоторые известные задачи и простые математические темы попали на киноэкран: математике посвящены, в частности, фильмы «Маленький человек Тейт» (1991), «Куб» (1997), «Мёбиус» (1996), «Пи» (1998), «Энигма» (2001) и многие другие. Однако существует фильм, все действие в котором вращается вокруг математики, — это «Западня Ферма» (2007) режиссеров Луиса Пьедраиты и Родриго Сопеньи. В фильме снимается блестящий актерский ансамбль, а герой Алехо Саураса, молодой специалист с фамилией Галуа (подсказка для внимательного зрителя), играет особую роль — он нашел доказательство гипотезы Гольдбаха. К сожалению, доказательство было украдено, о чем сообщается в начале фильма.

Сюжет фильма полон неожиданных поворотов, один из которых (по всей видимости, он взят из рассказа Эдгара Аллана По) заключается в том, что герои фильма заперты в комнате со сдвигающимися стенами. Эта драматическая история — лишь сюжет фантастического фильма: еще никому не удалось достаточно близко подойти к доказательству гипотезы Гольдбаха. Галуа признает, что его доказательство было ошибочным, однако другой персонаж, по фамилии Гильберт (его роль исполняет Луис Омар), по всей видимости, находит корректное доказательство. К сожалению, Гильберт погибает, а его выкладки оказываются на дне реки. На сегодняшний день гипотеза Гольдбаха по-прежнему не доказана и ждет своего укротителя.

Те, кто страдает бессонницей, обычно считают овец, чтобы заснуть. Математики богослов Блез Паскаль(1623–1662) нашел для себя другой способ призвать сон. В конце жизни он практически полностью посвятил себя богословию, оставив в стороне науку, которая до того была его основным занятием. При этом Паскаль страдал от бессонницы, которая не отступала, сколько бы овец он ни сосчитал. По всей видимости, недостаток сна стал причиной постоянных головных болей мыслителя, а во времена, когда еще не знали о болеутоляющих, это было настоящим мучением.