Иэн Стюарт - Математические головоломки профессора Стюарта

– Нет-нет, Ватсап! Я не предлагал вам попробовать свой метод на числе 111.

– Ох. А я полагал…

– Сколько раз я говорил вам, Ватсап: «Никогда ничего не полагайте!» Да, на первый взгляд эта загадка связана с числом 37, но на самом деле это, как бы это сказать, побочный эффект. Я предлагал вам посмотреть, как число 111 соотносится с числом 37.

Ответ см. в главе «Загадки разгаданные».

Из-за большого потока машин автобус, следующий из Эдинбурга в Лондон, проходит расстояние в 400 миль за 10 часов со скоростью 40 миль в час. На обратный путь у него уходит 8 часов со скоростью 50 миль в час. Какова средняя скорость автобуса за все время пути?

Очевидный ответ – 45 миль в час, среднее арифметическое между 40 и 50, для получения которого числа складывают, а сумму делят пополам. Однако в целом автобус проезжает 800 миль за 18 часов, и средняя скорость при этом равна 800/18 = 44 4/ 9миль в час.

Как это может быть?

Ответ см. в главе «Загадки разгаданные».

Головоломку без дополнительных указаний придумали Джерард Баттерс, Фредерик Хенле, Джеймс Хенле и Колин МакГоги. Это вариант судоку, который мне нравится называть псевдоку без дополнительных указаний. Вам предлагается решить еще четыре такие головоломки. Правила:

• Каждая строка и каждый столбец должны содержать каждое из чисел 1, 2, 3, …, n ровно по одному разу, где n – размер квадрата.

• Числа в каждой из областей, обведенных жирной линией, должны при сложении давать одну и ту же сумму. Я выписал значение этой суммы над каждым квадратом, чтобы избавить вас от необходимости искать ее самостоятельно. Все головоломки, кроме последней, имеют единственное решение, а последняя – два симметричных варианта.

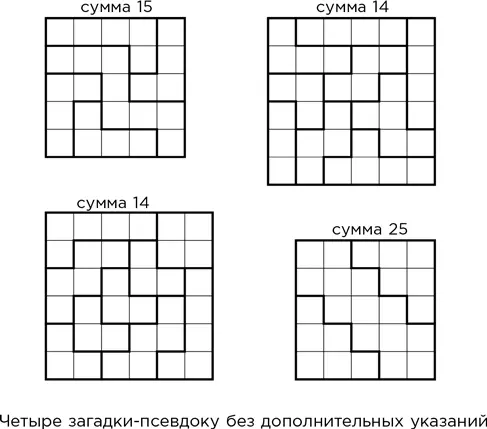
Ответы и ссылку на дополнительные материалы см. в главе «Загадки разгаданные».

Треугольные числа 1, 3, 6, 10, 15 и т. д. определяются сложением последовательных чисел, начиная с 1:

1 = 1;

1 + 2 = 3;

1 + 2 + 3 = 6;

1 + 2 + 3 + 4 = 10;

1 + 2 + 3 + 4 + 5 = 15

и т. д. Для таких чисел существует формула:

1 + 2 + 3 + … + n = n ( n + 1)/2.

Чтобы доказать ее, можно, в частности, записать сумму дважды, примерно так:

1 + 2 + 3 + 4 + 5;

5 + 4 + 3 + 2 + 1.

Из этой записи видно, что числа в вертикальных столбцах при сложении дают одно и то же, в данном случае 6. Поэтому удвоенная сумма равна 6 × 5 = 30, а сумма равна 15. Если проделать то же самое с числами от 1 до 100, все получится примерно так же: будет 100 колонок, дающих при сложении сумму 101, так что сумма первых 100 чисел должна составлять половину от 100 × 101, то есть 5050. В более общем случае при сложении первых n чисел мы получаем половину от n ( n + 1). Формула готова.

Существует формула и для суммы квадратов, но более сложная:

1 + 4 + 9 + … + n ² = n ( n + 1) (2 n + 1)/6.

А вот с кубами происходит нечто поразительное:

1³ = 1;

1³ + 2³ = 9;

1³ + 2³ + 3³ =36;

1³ + 2³ + 3³ + 4³ = 100;

1³ + 2³ + 3³ + 4³ + 5³ = 225.

Результаты здесь – квадраты соответствующих треугольных чисел.

Почему в результате суммирования кубов получаются квадраты? Можно найти формулу и доказать таким способом все, что нам нужно, но существует очень аккуратное наглядное доказательство того, что 1³ + 2³ + 3³ + … + n ³ = (1 + 2 + 3 + … + n )², для которого не нужны никакие формулы.

На рисунке показан один квадрат со стороной 1, два квадрата со стороной 2 (образующие куб 2 × 2 × 2), 3 квадрата со стороной 3 (куб 3 × 3 × 3) и т. д. Так что суммарная площадь этой фигуры представляет собой сумму последовательных кубов. Следуя вдоль одной из сторон (к примеру, верхней), видим 1 + 2 + 3 + 4 + 5, то есть сумму последовательных чисел. Но площадь квадрата равна квадрату его стороны. Готово!

Если вам непременно нужна формула, то мы знаем, что (1 + 2 + 3 + … + n ) = n ( n + 1)/2, а возведение в квадрат дает 1³ + 2³ + 3³ + … + n ³ = n ² ( n + 1)²/4.

Сомс передал мне конверт и поднял в руке извлеченное из него письмо.

– Проверка на наблюдательность, Ватсап. Кто, по-вашему, мог прислать мне это?

Я поднес конверт к свету, оглядел марку и штемпель, понюхал, исследовал клей в том месте, где письмо было запечатано.