Иэн Стюарт - Математические головоломки профессора Стюарта

We present a mnemonic to memorise a constant so exciting that Euler exclaimed: '!' when first it was found, yes, loudly '!'. My students perhaps will compute e , use power or Taylor series, an easy summation formula, obvious, clear, elegant [13] Замечание в предыдущем примечании касается и этого перевода: «Мы представляем мнемоническое правило для запоминания постоянной столь замечательной, что Эйлер воскликнул: "!", когда она была найдена, да, громко воскликнул"!". Мои студенты, возможно, вычислят e при помощи степени или ряда Тейлора по простой формуле суммирования, очевидной, ясной, элегантной». – Прим. пер. .

«Простая формула суммирования», упомянутая в тексте, такова:

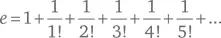
и так до бесконечности. Теперь знак! обозначает факториал

n ! = n × ( n – 1) × … × 3 × 2 × 1.

Существует бесконечно много натуральных чисел, которые можно выразить в виде суммы трех квадратов двумя разными способами: a ² + b ² + c ² = d ² + e ² + f ². Но возможны и дальнейшие выводы. Вот поразительный пример:

Это соотношение сохраняется, если мы будем последовательно убирать из каждого числа крайнюю левую цифру:

23789² + 61945² + 42864² = 42868² + 61943² + 23787²;

3789² + 1945² + 2864² = 2868² + 1943² + 3787²;

789² + 945² + 864² = 868² + 943² + 787²;

89² + 45² + 64² = 68² + 43² + 87²;

9² + 5² + 4² = 8² + 3² + 7².

Оно сохраняется также, если последовательно убирать из каждого числа крайнюю правую цифру:

12378² + 56194² + 64286² = 24286² + 76194² + 32378²;

1237² + 5619² + 6428² = 2428² + 7619² + 3237²;

123² + 561² + 642² = 242² + 761² + 323²;

12² + 56² + 64² = 24² + 76² + 32²;

1² + 5² + 6² = 2² + 7² + 3².

А также если мы будем убирать цифры одновременно с двух сторон:

2378² + 6194² + 4286² = 4286² + 6194² + 2378²;

37² + 19² + 28² = 28² + 19² + 37².

Эту математическую загадку прислали мне Молой Де и Нирмалья Чаттопадхьяй, объяснившие простую, но умную идею, на которой все это основано. Сможете ли вы уподобиться Хемлоку Сомсу и раскопать этот секрет?

Ответ см. в главе «Загадки разгаданные».

– Как любопытно! – заметил я, размышляя вслух.

– В мире много любопытного, Ватсап, – отозвался Сомс, дремавший, как мне казалось, в своем кресле. – Что именно вы имеете в виду?

– Я взял число 123 и повторил его шесть раз, – объяснил я.

– И получили 123123123123123123, – пренебрежительно сказал Сомс.

– Ну да, но я еще не закончил.

– Вы, несомненно, умножили это число на 37, – сказал великий детектив, вновь подрывая мою убежденность в том, что я могу сказать что-нибудь новое для него.

– Да! Умножил! И вот я получил… нет, Сомс, не прерывайте меня, пожалуйста… вот ответ… 4555555555555555551, и цифра 5 в нем повторяется много-много раз.

– И это любопытно?

– Без сомнения. Причем если один такой пример может быть случайным совпадением, то в данном случае все это не случайно. Нечто подобное происходит и в тех случаях, когда я беру не 123, а 234, или 345, или 456. Взгляните! – и я показал ему свои расчеты:

234234234234234234 × 37 = 8666666666666666658;

345345345345345345 × 37 = 12777777777777777765;

456456456456456456 × 37 = 16888888888888888872.

– И не только это: если я повторю 123, или 234, или 345, или 456 какое-то другое число раз и умножу это на 37, то в ответе опять же будет много-много повторений одной и той же цифры, а нарушения будут только по бокам.

– Я склонен думать, – пробормотал Сомс, – что структура числа 123, 234, 345 и т. д. не имеет значения. Другие числа вы пробовали?

– Я пробовал 124, и ничего не получилось. Взгляните:

124124124124124124 × 37 = 4592592592592592588.

– Цифры здесь повторяются блоками по три, но мне это не кажется удивительным – ведь и первое число имеет такую же структуру.

– 486 вы пробовали?

– Нет… ну вообще-то, поскольку с 124 не получается, мне не кажется… Ну хорошо, хорошо, – я вернулся к своему блокноту и записал новый расчет. – Как любопытно! – воскликнул я вновь, увидев ответ:

486486486486486486 × 37 = 1799999999999999982.

Вдохновленный новым успехом, я попробовал еще несколько случайных трехзначных чисел, выписывая их по несколько раз подряд и умножая на 37. Иногда результат содержал множество повторений одной и той же цифры, чаще нет. Я показал Сомсу результаты своей работы и признался:

– Я в недоумении.

– Загадка, несомненно, разрешится, – ответил Сомс, – если вы рассмотрите число 111.

Я записал

111111111111111111 × 37 = 4111111111111111107

и уставился на получившееся число. Минут через 20 Сомс поднялся, заглянул мне через плечо и иронично покачал головой.