Иэн Стюарт - Математические головоломки профессора Стюарта

– Вижу, это и правда так.

– Вы видите, Ватсап, но вы не замечаете . Наблюдение начинается с расспросов, которые дают материал для дедукции. Я сейчас занимаюсь расспросами. При каких обстоятельствах ваши кошки дерутся? Будьте точны, от этого зависит успех или неудача нашего замысла.

– Они дерутся только в помещении, – ответил я, немного поразмыслив.

– Но тогда дом может в любой момент взлететь на воздух!

– Нет, мои кошки могут быть совершенно мирными, если удастся избежать некоторых их сочетаний.

Я записал на листе бумаги несколько условий.

• Если Ветрянка и Аневризма находятся в помещении вместе, они дерутся, если рядом нет Геморроя. Если Геморрой и Ботулизм находятся в помещении вместе, они дерутся, если рядом нет Аневризмы.

• Если Аневризма и Геморрой находятся в помещении вместе, они дерутся, если рядом нет Ботулизма или Ветрянки (или их обоих).

• Если Ветрянка и Геморрой находятся в помещении вместе, они дерутся, если рядом нет Ботулизма или Аневризмы (или их обоих).

• Если Аневризма или Ботулизм остаются в помещении поодиночке, они вообще отказываются выходить наружу.

Как Сомсу и Ватсапу выманить кошек наружу, не вызвав при этом взрыв? Одновременно в кошачью дверцу может протиснуться лишь одно животное. Забудьте о тривиальных ходах, когда какая-то из кошек выходит наружу и ее тут же возвращают обратно. Однако при необходимости любую из кошек в процессе выманивания можно в нужный момент втолкнуть обратно через ту же дверцу.

Ответ см. в главе «Загадки разгаданные».

Вот настоящая математическая загадка – простая задача, решение которой пока ускользает от ученых не хуже, чем преступный гений Могиарти.

Дается стопка круглых блинов разных неповторяющихся размеров. Ваша задача – поменять порядок блинов таким образом, чтобы они располагались снизу вверх в порядке убывания диаметра. Единственное действие, которое вам разрешается производить, – это вставить условную лопаточку под один из блинов стопки, поднять стопку, которая оказалась сверху, и перевернуть ее целиком. Вы можете повторять эту операцию столько раз, сколько потребуется, и произвольно выбирать место, куда вставлять лопаточку.

Приведем пример с четырьмя блинами. Для их упорядочивания требуется три переворота.

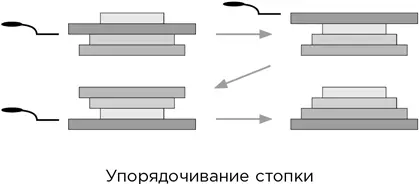
Вот несколько вопросов для вас.

1. Любую ли стопку из четырех блинов можно упорядочить не более чем за три переворачивания?

2. Если нет, то каково наименьшее число переворачиваний, при помощи которых можно упорядочить любую стопку из четырех блинов?

3. Определите для n -го блина число Pn – наименьшее число переворачиваний, при помощи которых можно упорядочить любую стопку из n блинов. Докажите, что Pn всегда конечно. То есть что любую стопку блинов можно упорядочить при помощи конечного числа переворачиваний.

4. Найдите P n для n = 1, 2, 3, 4, 5. Я остановился на n = 5, потому что здесь мы уже имеем 120 различных вариантов стопки, все из которых нужно рассмотреть, а это, говоря откровенно, уйма работы.

Ответы на вопросы, а также то, что еще известно об этой задаче, см. в главе «Загадки разгаданные».

В продолжение кулинарной темы существует забавный фокус, который вы можете проделать с суповой тарелкой или другим похожим предметом. Начните с того, что поставьте тарелку на пальцы примерно так, как это делает официант, подавая кушанья. Затем объявите зрителям, что вы сейчас проделаете поразительный трюк: сделаете полный круг рукой, все время удерживая тарелку в горизонтальном положении.

Для этого сначала заверните руку внутрь – так чтобы тарелка оказалась примерно под мышкой. Затем продолжайте двигать тарелку по кругу, но руку поднимите над головой. Все естественным образом повернется в исходную позицию, и тарелка не упадет, несмотря на то что вы ее не придерживаете.

Видео трюка с тарелкой (суповой) можно найти в Интернете, к примеру на сайте

http://www.youtube.com/watch?v=Rzt_byhgujg,

где его называют балийским трюком с чашей и связывают с балийским танцем, где вместо тарелки используется чаша с жидкостью. Аналогичный филиппинский танец, где задействованы винные бокалы (по два на человека, по одному в каждой руке), можно увидеть на YouTube по адресу

http://www.youtube.com/watch?v=mOO_IOznZCQ