Рафаель Роузен - Математика для гиков

Кто бы мог подумать, что iPod и математика тесно связаны друг с другом? Оказывается, когда вы загружаете песню на компьютер или проигрываете цифровой музыкальный файл на плеере, вы пользуетесь математическим уравнением под названием преобразование Фурье.

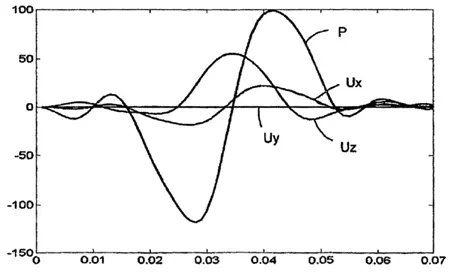
Звучит странно, но представьте, что это своего рода инструмент: в сущности, он разделяет сложные волны на множество маленьких и соединяет простые волны обратно в сложные. И это могут быть почти любые виды волн, включая звуковые и световые. Когда звукорежиссеры хотят конвертировать аудиозапись в МР3-файл, они используют преобразование Фурье, чтобы выбрать отдельные частоты звуковой волны и отметить их амплитуду в каждый момент времени. Затем, если они хотят сжать файл, чтобы его было легче передавать через Интернет, они могут удалить частоты, которые человеческое ухо не может услышать. С другой стороны, звук на виниловой пластинке представляет собой цельную звуковую волну, частоты на ней нетронуты.

Человеческое ухо также может выполнять преобразование Фурье. В любой момент одна сложная звуковая волна входит в ухо, где происходит вибрация барабанной перепонки, и производит электрические волны, которые мозг потом анализирует и преобразовывает. Но вы никогда не слышите эту одну волну, вместо этого вы слышите человека, который слева от вас разговаривает по телефону, автобус, который сигналит автомобилю справа, щебечущую над вами птицу, которая сидит на дереве. Эта одна волна была разбита на составные части, и теперь вы можете выявить отдельные частоты и звуки и тем самым лучше взаимодействовать с миром.

Преобразование Фурье также можно встретить и в архитектуре, особенно в сейсмоопасных районах. Как и любой другой объект, каждое здание в городе вибрирует на своей собственной частоте. Представим здание в городе, в котором произошло землетрясение. Если колебания от землетрясения совпадают с естественным колебанием здания, колебания усилятся, и у такого здания вероятность разрушения становится выше. (Частота и сила колебаний – это два разных измерения.) Чтобы избежать разрушения, инженеры могут использовать преобразование Фурье для анализа отдельных частот типичных землетрясений в конкретном месте и потом «настроить» здание так, чтобы его частоты не совпадали с частотами землетрясений, которые чаще всего происходят в районе. Математика может буквально спасать города от разрушения.

Преобразование Фурье названо в честь Жана Батиста Жозефа Фурье, французского математика (1768–1830). Он его разработал, когда пытался определить, как тепло передается между твердыми телами.

Вы или ярый сторонник карт Google, или приверженец традиционных бумажных карт, но карты окружают нас повсюду. Они полезны и, несмотря на иногда возникающие трудности со складыванием, очень удобны. Зачастую они еще и очень красивые. (Посмотрите на карты из Средневековья, чтобы получить представление о художественности, которая вкладывалась в создание карт.) Карты также являются источником для одной из самых известных идей в математике: проблемы четырех красок.

Фрэнсис Гатри, английский студент, изучающий математику, впервые предложил проблему в 1852 году, когда пытался раскрасить карту округов Англии. Понимая, что ему необходимо всего четыре цвета, он задался вопросом, а нельзя ли применить это правило ко всем картам, даже к тем, которые еще не были созданы. Точнее говоря, Гатри интересовало, можно ли раскрасить карту, используя не больше четырех цветов, так, чтобы у двух граничащих территорий – округов, штатов, стран, чего угодно – не совпадали цвета. (Такие две территории должны иметь четкую границу. Если территории граничат углами, как штаты Юта и Нью-Мексико, то они не в счет.) Доказательство было наконец предоставлено в 1976 году, спустя 124 года после того, как Гатри задал этот вопрос, Кеннетом Аппелем и Вольфгангом Хакеном, математиками из Иллинойсского университета в Урбане-Шампейне. И хоть это было значительное достижение, доказательство вызвало неоднозначную реакцию в математическом сообществе, так как оно использовало компьютер.