Кьяртан Поскитт - Математика для взрослых

Если перед открывающей скобкой стоит число, то на него умножается все, что находится внутри скобок.

Добавляем буквы

Наверное, вам уже не терпится перейти к решению хитро­умных дифференциальных уравнений, однако начнем с ма­лого.

Прогуливаясь по улице, вы неожиданно встречаете Малькольма, который пребывает в легком шоке. Он только что водил маму в кофейню Barstucks, где они выпили по чашке кофе, и в результате из 10 фунтов, которые он брал с собой, осталось всего 1,20 фунта. Сколько же стоила каждая чашка? Вот что нам известно: 10 фунтов минус цена двух чашек кофе = 1,20 фунта

Мы сэкономим массу типографской краски, если обозначим цену одной чашки кофе буквой c . Из этого следует, что цена двух чашек кофе составит 2 × c , но для удобства мы просто напишем 2 c .

Что ж, давайте составим уравнение и посмотрим, как быть дальше.

10 – 2c = 1,20

Нам нужно, чтобы слева от знака равенства была только буква c . Для начала перенесем 10 фунтов на другую сторону, поменяв знак на минус: –2c = 1,20 – 10

Минус перед 2 c выглядит не слишком привлекательно, по­этому избавимся от него, умножив обе части уравнения на (–1). В результате каждый знак «+» поменяется на «–», а каждый знак «–» на «+»: 2c = 10 – 1,20

Теперь подсчитаем 10 – 1,20 = 8,80, тогда

2с = 8,80

Поскольку нам нужна только одна с , разделим обе части на 2, и ответ готов: с = 4,40 фунта

4,40 фунта за чашку кофе? Неудивительно, что Малькольм был в шоке!

Что можно и чего нельзя

В алгебре есть еще несколько на первый взгляд странных правил, поэтому, чтобы они стали понятнее, представим себе множество одинаковых коробков спичек. В каждом содержится m спичек, так что если мы отложим в сторону три коробка, общее количество спичек в них составит 3 × m , или просто 3 m . Число 3 здесь — коэффициент при m .

Теперь, разобравшись с коробками, перейдем к правилам и выясним, как их применять к нашим спичкам.

1.-Коэффициент можно умножать на число

Если добавить еще одну стопку из трех коробков...

… то 2 стопки по 3 m в сумме дадут 6 m .

2.-Прибавлять число к коэффициенту нельзя

Если вы где-то нашли три спички...

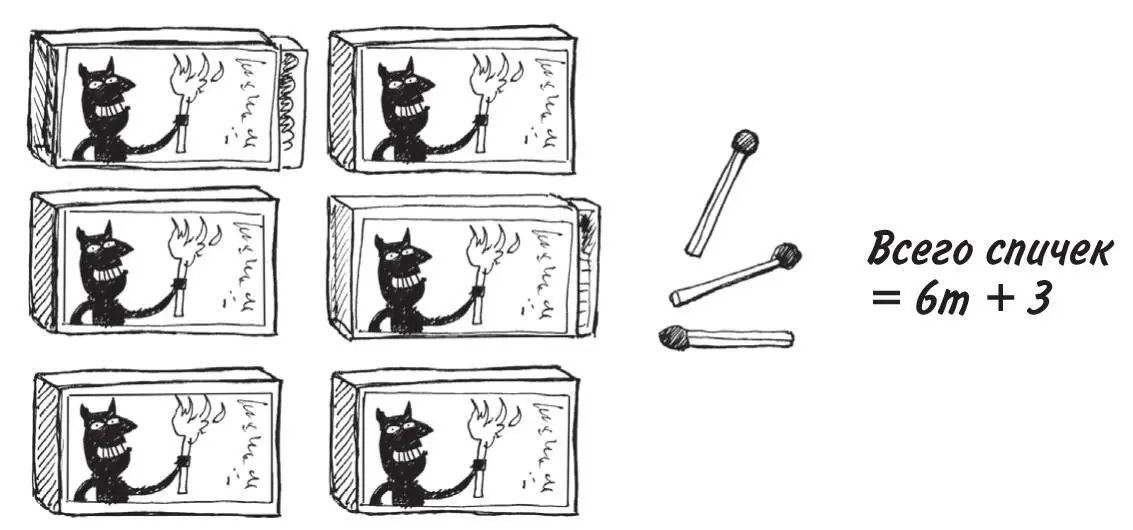
Видите, теперь у нас 6 m + 3 спички. Нельзя прибавлять 3 к 6, чтобы получить 9 m !

3.-Коэффициенты можно складывать, если при них одна и та же буква

Если взять еще два коробка...

Как видите, складывать 6 m и 2 m , чтобы получить 8 m , можно, но 3 прибавить к 8 m по-прежнему нельзя.

Вот еще три правила. Не волнуйтесь, если сейчас они покажутся вам непонятными, чуть позже мы их применим, и все прояснится.

4.-Когда знак «минус» стоит перед скобками, избавляясь от них, надо поменять все знаки внутри скобок на противоположные

В выражении вроде 3 − (2 x − 4) все, что внутри скобок, следует умножить на –1. Избавившись от скобок, вы получите 3 − 2 x + 4. Вместо +2 х стало –2 х , а вместо –4 стало +4.

5.-Если умножить букву на саму себя, получается буква в квадрате

Таким образом, y × y превратится в y 2(что такое числа в квадрате, мы обсуждали в разделе «Квадраты и квадратные корни»), а 4 y × 3 y — в 12 y 2. Коэффициенты перемножаются, а у буквы появляется знак квадрата.

6.-При перемножении разных чисел и букв числа умножаются, а буквы пишутся вместе

Поэтому 2 x × 4 y = 8 xy . Такие ситуации часто возникают при умножении содержимого скобок, например: 3 p (7 q − 2 p ) = 21 pq − 6 p 2.

Итак, давайте посмотрим, как это все может нам пригодиться.

Разгадка тайн математики с помощью алгебры

Алгебра бывает крайне полезна при решении задач и головоломок. Вот вам кое-что для начала.

Земельная афера

Бэтчап Билдингз решил приобрести надел земли у фермера Шарпа. Обе стороны сошлись на том, что это должен быть квад­ратный участок 20 м × 20 м, то есть площадью 400 квадратных метров, или м 2. Однако приехав осмотреть землю, Бэтчап увидел, что участок имеет прямоугольную, а не квадратную форму!