Крис Уоринг - Формулы на все случаи жизни. Как математика помогает выходить из сложных ситуаций

n(n + 4) = 45.

Прежде чем решить уравнение, нужно избавиться от скобок. Чтобы облегчить задачу, предлагаю представить ее в виде прямоугольника, одна сторона которого равна n метров (м), другая – n + 4 метров. Он будет выглядеть так:

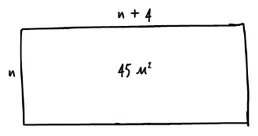
Поделив длинную сторону на два отрезка, один из которых имеет длину n метров, а другой – 4 метра, получим прямоугольник и квадрат:

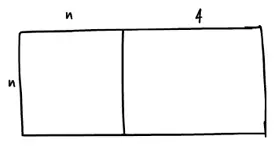
Теперь можем определить площадь каждой фигуры:

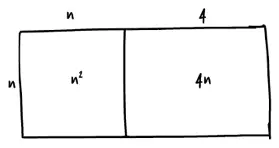
Таким образом, общая площадь прямоугольника получается равной n 2+ 4n, что составляет 45:

n 2+ 4n = 45.

Видите? Скобок больше нет! Процесс называется умножением на скобку, или ее раскрытием. Полученное квадратное уравнение решается с помощью формулы, приведенной в подразделе «Решение уравнений».

Алгебраический метод, противоположный раскрытию скобок, может быть полезен при решении уравнений или преобразовании формул. Рассмотрим на примере:

4 × 3 + 5 × 3 = (4 + 5) × 3.

Проведя операции, получим:

12 + 15 = 9 × 3

27 = 27.

Равенство истинно. Истинно и то, что мы могли бы заменить тройку любым другим числом и получить: четыре раза по столько-то плюс пять раз по столько-то – это девять раз по столько-то. Если вместо «столько-то» мы возьмем букву, выражение станет алгебраическим, а задача примет такой вид:

4a + 5a = (4 + 5) a.

Обе части уравнения здесь, конечно, равны 9а. Такой процесс называется вынесением за скобки общего множителя. Можем пойти еще дальше и заменить 4 и 5 на другие неизвестные:

Xa + Ya = (X + Y)a.

Это умение – выносить общий множитель за скобки – пригодится при решении уравнений, где одно и то же неизвестное встречается несколько раз.

Надеюсь, что вышеизложенные основы помогли вам освежить воспоминания, и теперь вы готовы рассмотреть первую ситуацию. Все еще не уверены в собственных силах? Не волнуйтесь. В каждой главе мы внимательно, шаг за шагом и с подробными объяснениями разберем любую возможную проблему. Да, и никаких экзаменов. Возможно, вам это и не приходило в голову после школы, но, прочитав эту книгу, вы поймете, что на самом деле для каждого случая есть свое уравнение.

Как частный консультант по безопасности вы не имеете себе равных: ряд недавних громких дел даже привлек внимание международных СМИ. Но как только на пороге вашего офиса появляется разодетая по последней парижской моде дама, вы тут же отменяете все свои встречи и, предложив ей чай/кофе, соглашаетесь выяснить, кто из сотрудников Лувра подменяет шедевры практически идеальными копиями. Бюджет, который музей выделяет на безопасность, сильно ограничен. Вместе с заказчицей вам предстоит придумать, как при минимальном количестве охранников уберечь картины, скульптуры и прочие художественные ценности, представленные на выставке, которая недавно открылась… ну, скажем, в зале математического искусства [2] Выдумка автора. – Прим. пер. . При этом заказчица требует, чтобы каждая часть экспозиции находилась под постоянным наблюдением хотя бы одного охранника. Как эффективно решить поставленную задачу?

Мы должны обратиться к математической логике и попытаться мыслить геометрически. Давайте начнем рассуждать о помещении и его безопасности на языке математики. Итак: обозначьте необходимое количество охранников буквой g, а затем посмотрите, получится ли уменьшить это значение. Прежде всего вам нужно разобраться в многоугольниках (полигонах).

Многоугольники – плоские фигуры с прямыми сторонами. В большинстве случаев план помещения представляет собой совокупность многоугольников, которые в основном (но не всегда, что можно увидеть на представленной ниже планировке) имеют прямые углы.

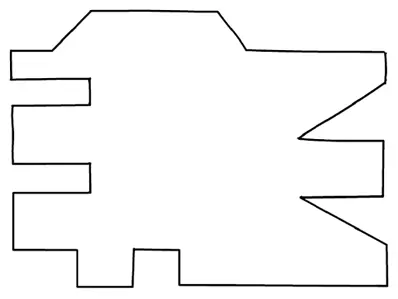
Многоугольники принято называть по количеству сторон. Треугольник представляет собой многоугольник с тремя сторонами (для полигона это число сторон является минимально возможным). Если склеить два треугольника, сторона к стороне, получится четырехсторонняя фигура, известная как четырехугольник.