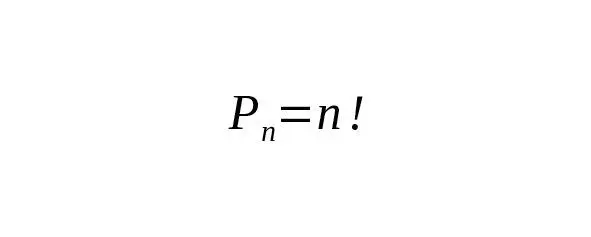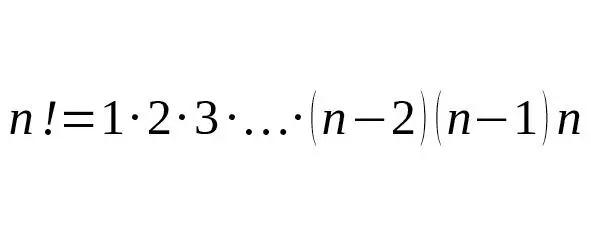Дмитрий Кудрец - Занимательная комбинаторика

© Дмитрий Кудрец, 2022

ISBN 978-5-0050-7620-5

Создано в интеллектуальной издательской системе Ridero

В повседневной жизни мы часто сталкиваемся с ситуациями, когда нам необходимо рассадить гостей за столом, составить букеты из имеющихся цветов, подсчитать количество выигрышных билетов в лотерее и т. д. Но задумывались ли вы, сколькими вариантами мы можем это сделать? На этот вопрос помогает ответить комбинаторика – раздел математики, изучающий задачи выбора и расположения элементов из некоторого множества в соответствии с заданными правилами.

Формулы и методы комбинаторики широко используются в теории вероятностей для подсчета вероятности случайных событий.

Комбинаторика как самостоятельная наука появилась в XVIII веке. Рождение комбинаторики связано с трудами Блеза Паскаля и Пьера Ферма по теории азартных игр. Большой вклад в развитие комбинаторики методов внесли Готфрид Вильгельм Лейбниц, Яков Бернулли, Леонард Эйлер и другие выдающиеся ученые.

Однажды в выходной день Маша решила навести порядок в своих игрушках и рассадить в ряд медвежонка, куклу и львёнка.

Вначале она рассадила их так:

Но ей не понравилось, что медвежонок сидит рядом со львёнком. Тогда Маша пересадила игрушки следующим образом:

Но и тут Маша не смогла определиться, кто должен сидеть справа от куклы – львёнок или медвежонок?

Так бы Маша и продолжала бы переставлять игрушки с места на место, если бы в комнату не вошел Машин папа.

– Ты чем это занимаешься? – поинтересовался он у Маши.

– Да вот, – грустно вздохнула Маша, – пытаюсь расставить игрушки, но у меня что-то не получается. Столько много разных вариантов, а мне ни один не нравится.

– Допустим, – не согласился папа, – что вариантов не так уж и много. У тебя три игрушки, значит, вариантов всего шесть.

– Как ты так быстро посчитал? – удивилась Маша.

– Есть такая наука, – пояснил папа, – комбинаторика. Она и занимается подсчетом различных вариантов перестановок. Допустим у тебя всего две игрушки – медвежонок и кукла. Их можно переставить только двумя способами:

или

Если у тебя три игрушки, то это можно сделать уже шестью способами:

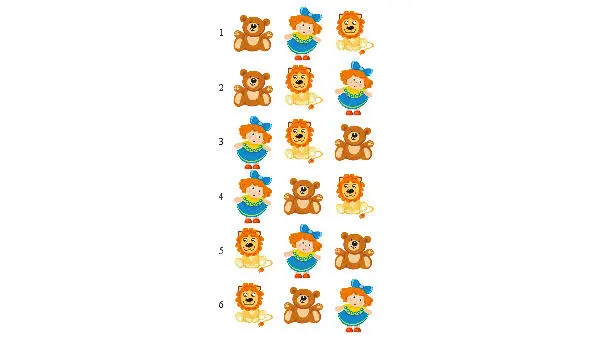
– А если у меня четыре игрушки? – спросила Маша.

– Тогда существует 24 варианта различных способов их перестановки. В комбинаторике такие упорядочения множества, состоящего из определенного количества элементов, так и называют – перестановками . Особенностью перестановок является то, что в них должны участвовать все элементы данного множества.

Количество всех возможных перестановок можно найти по формуле, где n – количество элементов данного множества.

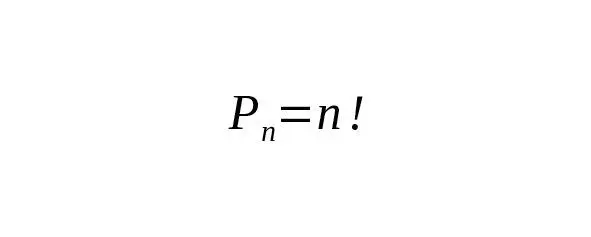
Символ n ! называется факториалом и обозначает произведение всех целых чисел от 1 до n .

.

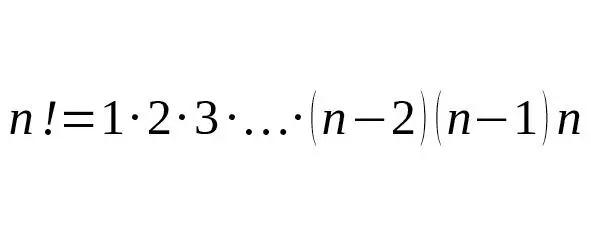
Например, 3!=1∙2∙3=6. 4!=1∙2∙3∙4=24.

При вычислении факториала принято считать, что 0!=1, 1!=1.

– А если у меня пять игрушек? – не унималась Маша.

– В таком случае у тебя 1∙2∙3∙4∙5=120 вариантов перестановок.

– Так много? – удивилась Маша.

– А если множество состоит из 6 элементов, – продолжал папа, – то число перестановок будет равняться 720. Для 7 элементов число перестановок будет равно 5040, для 8 – 40320 и так далее. Чем больше число элементов, тем больше число перестановок.

– А если вместо пяти игрушек взять пять конфет? – спросила Маша. – Число перестановок изменится?