Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Это было непросто. Любой, кто сбрасывал камень с моста, знает, что камни падают быстро. Чтобы следить за камнем в каждый момент его падения, нужны очень точные часы, а таких во времена Галилея не было, да и несколько хороших видеокамер не помешали бы, но и они отсутствовали в начале 1600-х годов.

Галилей придумал блестящее решение: он замедлил движение. Вместо бросания камня с моста он пускал шар по наклонному скату. На языке физики он известен как наклонная плоскость, хотя во время первоначальных экспериментов Галилея это был длинный тонкий кусок дерева с прорезанным желобком для шара. Когда ученый уменьшал наклон почти до горизонтального, он мог замедлить движение шара до желаемой скорости, что позволяло ему измерять, где находится шар в каждый момент времени, обходясь инструментами, доступными в то время.

Чтобы определить время спуска шара, он использовал водяные часы. Они работали как секундомер: в начальный момент физик открывал вентиль и вода начинала с постоянной скоростью поступать по тонкой трубе в резервуар. В нужный момент он закрывал вентиль. Взвесив воду, накопившуюся в резервуаре за время спуска шара, Галилей мог количественно определить, сколько времени прошло, с точностью до «одной десятой удара пульса» [112], [113].

Он повторял эксперимент много раз, иногда меняя наклон ската, а иногда – расстояние, проходимое шаром. По его словам, он установил следующее: «Расстояния, пройденные за равные промежутки времени телом, падающим из состояния покоя, находятся между собой в таком же соотношении, как и нечетные числа, начинающиеся с единицы» [114].

Чтобы понятнее изложить этот закон больших чисел, предположим, что шар прокатится некоторое расстояние за первую единицу времени. Тогда за вторую единицу времени он прокатится втрое дальше, за третью – впятеро. . Это потрясающе! Нечетные числа 1, 3, 5 и так далее как-то связаны с тем, как предметы катятся вниз. И если падение – это предельный случай качения, когда наклон приближается к вертикали, то и для падения должно быть справедливо то же самое.

Мы можем только представить, как должен был обрадоваться Галилей, когда открыл это правило. Но обратите внимание, как он его сформулировал: словами, числами и соотношениями, а не буквами, формулами и уравнениями. Наша нынешняя манера использовать алгебру, а не разговорный язык, по тем временам казалась бы авангардным, новейшим, новомодным способом думать и говорить. Галилей так не думал и не выражался, да и читатели его бы не поняли.

Чтобы увидеть самые важные следствия из правила Галилея, давайте посмотрим, что произойдет при сложении последовательных нечетных чисел. За одну единицу времени шар прошел одну единицу расстояния. За следующую – еще три единицы расстояния, то есть в общей сложности 1 + 3 = 4 единицы с момента начала движения. После третьей единицы времени получаем 1 + 3 + 5 = 9 единиц расстояния. Обратите внимание на закономерность: числа 1, 4 и 9 – это квадраты последовательных целых чисел: 1 2 = 1, 2 2 = 4, 3 2 = 9. Таким образом, правило нечетных чисел Галилея, похоже, означает, что общее расстояние, пройденное падающим телом, пропорционально квадрату прошедшего времени.

Эту изящную связь между нечетными числами и квадратами можно доказать наглядно. Представьте нечетные числа как «уголки» из точек:

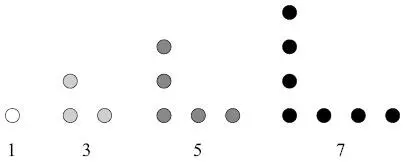
Теперь соедините их так, чтобы получился квадрат. Например, 1 + 3 + 5 + 7 = 16 = 4 × 4, поскольку мы можем сложить первые четыре уголка так, чтобы они образовали квадрат со стороной 4.

Наряду с законом о расстоянии, пройденном падающим телом, Галилей также открыл закон скорости. По его словам, скорость увеличивается пропорционально времени падения. Интересно здесь то, что ученый имел в виду мгновенную скорость, что кажется парадоксальным понятием. В книге «Две новые науки» он приложил немало усилий, чтобы объяснить, что при падении из состояния покоя тело не прыгает внезапно с нулевой скорости до какой-то более высокой, как полагали его современники. Наоборот, оно плавно проходит через все промежуточные скорости – бесконечное количество скоростей – за конечное время, начиная с нулевой и непрерывно увеличивая скорость при падении.

Итак, в этом законе падающих тел Галилей инстинктивно размышлял о мгновенной скорости – понятии дифференциального исчисления, с которым мы познакомимся в главе 6. В то время он не мог определить ее точно, но интуитивно понимал.