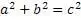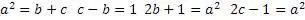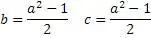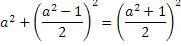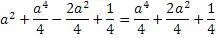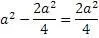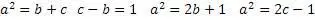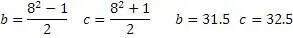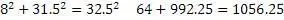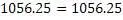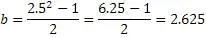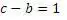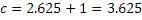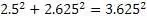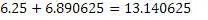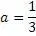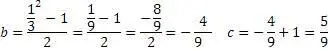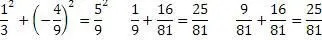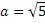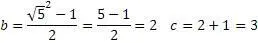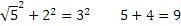Дмитрий Паршаков - Алгоритм решения 10 проблемы Гильберта

В 1900г. на 1 Международном математическом конгрессе, известный математик Давид Гильберт[1] поставил перед математиками всего мира 23 задачи. Эти задачи принято называть "Проблемами Гильберта".

Решением десятой проблемы Гильберта стало признание ее неразрешимости, доказанное советским математиком Ю.В.Матясевичем [2] в 1970г.

Доказательство неразрешимости Матиясевича признано как единственно допустимое, но возможно это не так.

Итак, для того, чтобы опровергнуть, либо подтвердить это доказательство нужно вначале напомнить задачу, определенную Д.Гильбертом в 10-й проблеме.

«Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах»

То есть нужно найти некий алгоритм, при помощи которого возможно находить натуральные (целочисленные) значения для произвольных неизвестных.

Самое известное уравнение Диофанта[3] это формула Пифагора[4].

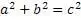
Известны также так называемые «тройки Пифагора», целочисленные значения для неизвестных «a,b,c»

3,4,5; 5,12,13; 7,24,25 и т.д. Эти тройки имеют два сходства: первое – квадрат первого числа равен сумме двух других чисел, второе – разница между вторым и третьим числом равна 1. Следовательно, можно предположить, что это не случайные совпадения. Исходя из этого, составим равенства

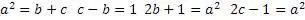
Теперь, используя все эти формулы, составим уравнения

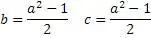
Подставим эти уравнения в формулу Пифагора

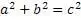
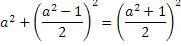
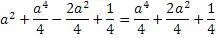
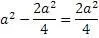
Получилось равенство значений правой и левой сторон уравнения. Это можно считать доказательством существования алгоритма нахождения натуральных значений «пифагоровых троек». Итак, обобщим формулы алгоритма и собственно получившийся алгоритм

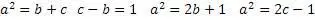
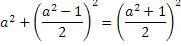
Но эти формулы диофантовы лишь для нечетных чисел, хотя при постановке в формулы четных чисел для «а» также можно найти значения двух других чисел «b» «c», эти значения будут рациональными, но не целыми числами.

Пример № 1

«а»= 8

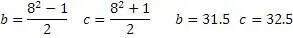
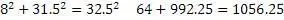
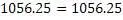
Также, применяя этот алгоритм, можно находить соответствующие значения «троек» для любых рациональных чисел.

Пример № 2

a=2,5

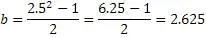
Так как закономерностью алгоритма является соотношение

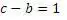
то значение «c» можно найти, добавив к числу «b» 1

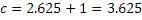
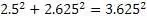
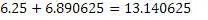
Алгоритм верен и для дробей

Пример № 3

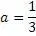
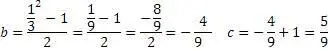
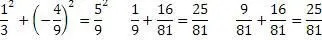
И для квадратных корней

Пример № 4

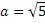
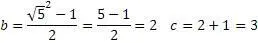
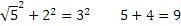
Применяя этот алгоритм, можно находить значения практически всех троек Пифагора.