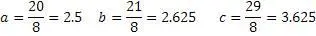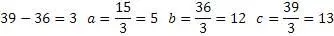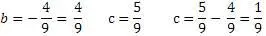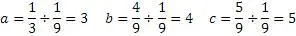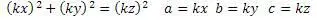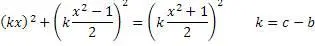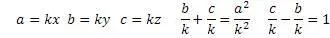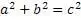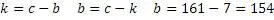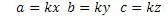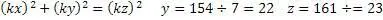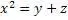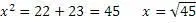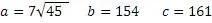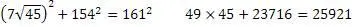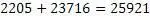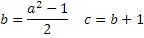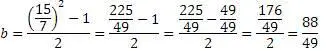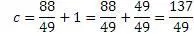Дмитрий Паршаков - Алгоритм решения 10 проблемы Гильберта

Однако существуют тройки, которые не подходят к этому алгоритму: 20,21,29; 12,35,37; 14,48,50; 15,36,39 и т.д.

Следовательно: этот алгоритм нельзя назвать единым способом нахождения всех Пифагоровых троек. Но не будем опускать руки. Разберем пример с числовой тройкой 20,21,29

Выше я привел пример с а=2.5, значения b и с были соответственно 2.625 и 3.625, если предположить, что число 20 это производная числа 2.5, то получится коэффициент равный 8, и следовательно числа 20,21,29 не являются взаимно простыми. Проверим это предположение

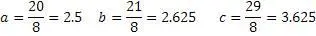
Коэффициент кратности исходного уравнения совпадает с разностью между «b» и «с». Чтобы выяснить совпадение это или закономерность, проверим другую тройку 15,36,39. Разница между «b» и «с» составляет 3

Пример № 5

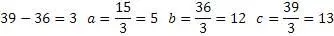
Получилась уже известная тройка 5,12,13, то есть удовлетворяющая условиям исходного или первичного алгоритма, что и требовалось подтвердить.

Остается еще один вопрос. При возведении числа в квадрат не важно, с каким знаком: плюсом или минусом, результат все равно будет иметь положительное значение. Это важно для подтверждения правильности алгоритма. В примере 3, число «b» имеет отрицательное значение, но если поменять знак ничего не изменится, и результат останется прежним. Если поменять знак числа b с минуса на плюс, разница между b и с, уменьшится в 9 раз

Пример № 6

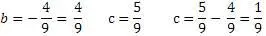
Исходя из вышеизложенного, можно предположить, что разница является коэффициентом кратности исходного уравнения. Для проверки этого предположения нужно разделить числа тройки на получившийся коэффициент.

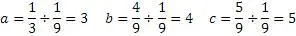
И вновь получилась уже известная тройка 3,4,5.

На основании полученных результатов, можно записать алгоритм кратности

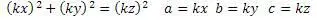
Осталось объединить получившиеся алгоритмы в один универсальный.

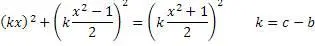
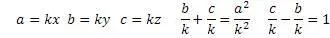
Теперь можно вычислять абсолютно все пифагоровы тройки, зная или задавая значение любого одного числа из тройки и задавая кратность уравнению.

Задача № 1

Найти значения чисел «а» и «b» в уравнении

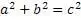
Условия задачи

Дано:

Значение числа «с»=161

Коэффициент кратности уравнения «k»=7

Воспользуемся формулами универсального алгоритма

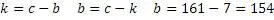
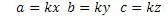
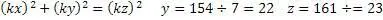
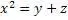
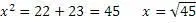
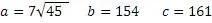
Проверим получившийся результат

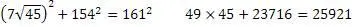
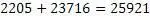
Задача решена, числа найдены.

Задача № 2

Требуется найти натуральные значения чисел «b» и «с» для уравнения

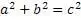
Условия задачи

Дано:

Воспользуемся формулами, для нахождения исходных «троек»

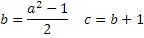
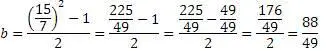
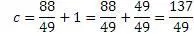
Подставим числа в формулу