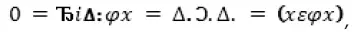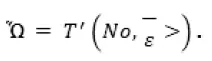Жюль Пуанкаре - Теорема века. Мир с точки зрения математики

Как бы то ни было, Бурали-Форти исходит из этого определения и после коротких вычислений приходит к уравнению

1εNO,

которое дает нам понять, что «один» есть число.

Так как нам теперь приходится иметь дело с определениями простых чисел, то мы напомним, что Кутюра также определил 0 и 1.

Что такое нуль? Это число элементов нулевого класса. А что такое нулевой класс? Это класс, который не содержит никакого элемента.

Определять нуль при помощи нулевого класса, а нулевой класс при помощи термина «никакой» – это значит поистине злоупотреблять богатством языка; поэтому Кутюра ввел усовершенствование в свое определение, написав:

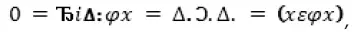
что обозначает: нуль есть число предметов, удовлетворяющих такому условию, которое никогда не выполняется.

Но так как «никогда» обозначает «ни в одном случае», то я не вижу значительного успеха в этой замене.

Спешу прибавить, что определение, которое Кутюра дает числу 1, более удовлетворительно.

«Один, – говорит он, – в сущности, есть число элементов класса, два любых элемента коего тождественны».

Это определение более удовлетворительно, как я сказал, в том смысле, что для определения понятия 1 автор не пользуется словом «один». Но зато он пользуется словом «два». И я боюсь, что если спросить у Кутюра, что такое «два», то он должен будет в ответе воспользоваться словом «один».

Вернемся к мемуару Бурали-Форти. Я сказал, что его заключения прямо противоположны выводам Кантора. Но однажды меня посетил Адамар. Разговор коснулся этой антиномии.

– Не кажется ли вам, – сказал я, – что рассуждение Бурали-Форти безупречно?

– Нет, напротив, я не вижу в нем никаких возражений Кантору. Кроме того, Бурали-Форти не имел права говорить о совокупности всех порядковых чисел.

– Простите, он имел это право, потому что всегда мог написать:

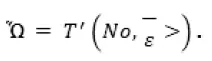
– Я хотел бы знать, кто бы мог ему в этом воспрепятствовать, и можно ли сказать, что предмет не существует, если его назвали Q?

Мои старания были тщетны, убедить Адамара я не мог (противоположное было бы, впрочем, очень прискорбно, так как он был прав). Потому ли это было, что я не говорил достаточно красноречиво на языке Пеано? Возможно; но, между нами говоря, я этого не думаю.

Таким образом, несмотря на весь этот пасиграфический аппарат, вопрос не был разрешен. Что это доказывает? Когда вопрос идет только о том, чтобы доказать, что один есть число, пасиграфия достаточна; но если представляется затруднение, если возникает антиномия, требующая разрешения, то пасиграфия становится бессильной.

Чтобы оправдать свои притязания, логика должна была преобразоваться. Народились новые логики, среди которых наиболее интересной является логика Рассела. Казалось бы, что в области формальной логики ничего нового нельзя сказать и что Аристотель давно узрел ее основы. Но поле действия, которое Рассел отводит логике, бесконечно шире, чем поле классической логики, и Рассел сумел высказать в этом отношении оригинальные и часто правильные взгляды.

Между тем как логика Аристотеля была преимущественно логикой классов и за исходную точку брала отношение субъекта к предикату, Рассел прежде всего подчиняет логику классов логике предложений. Классический силлогизм «Сократ – человек и т. д.» уступает место гипотетическому силлогизму: если А истинно, то В истинно, но если В истинно, то С истинно и т. д.; и эта идея, на мой взгляд, одна из наиболее счастливых, ибо классический силлогизм легко свести к гипотетическому, тогда как обратное превращение представляет затруднение.

Но это не все: логика предложений Рассела есть этюд о законах, по которым комбинируются союзы «если», «и», «или» и отрицание «не». Это значительное расширение старой логики. Свойства классического силлогизма без труда распространяются на гипотетический силлогизм, и в формах последнего легко узнаются схоластические формы. Мы находим здесь то, что является существенным в классической логике. Но теория силлогизма есть еще не что иное, как синтаксис союза «если» и, быть может, отрицания.

Присоединяя два других союза – «и» и «или», – Рассел открывает логике новую область. Знаки «и», «или» подчиняются тем же законам, что и знаки × и +, т. е. переместительному, сочетательному и распределительному законам. Таким образом, «и» представляет логическое умножение, тогда как «или» представляет логическое сложение. Это также весьма интересно.