Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

По словам Евклида, согласно теореме Пифагора, в равнобедренном прямоугольном треугольнике квадрат гипотенузы равен удвоенному квадрату каждого из катетов. Если длину катета считать за 1, какой будет длина гипотенузы?

Предположим, что ее длина составляет т/п метров:

m2/n2 = 2

Предположим m и n не имеют общего делителя и делятся друг на друга, тогда m или n должно быть нечетным. Так как m 2= 2n 2, то m 2четное и, следовательно, m тоже четное, то есть n — нечетное. Таким образом, мы можем подставить m = 2p. Следовательно, 4p 2= 2n 2; из этого выводится, что n 2= 2p 2, и значит, n четное. Выходит, что никакая дробь вида m/n не может выражать длину гипотенузы. Это соображение подчеркивает, что при любой единице измерения есть такие длины, которые не могут быть выражены числовым соотношением на основе этой единицы, в том смысле что не существует таких целых чисел тип, чтобы взятая т раз длина совпадала с взятой п раз единицей измерения. Метод Евклида используется и сегодня для доказательства иррациональности √2, однако ученые склонны считать, что он был добавлен в текст «Начал» значительно позже. В современных изданиях Евклида этот метод обычно опускается, и книга X оканчивается предложением 115.

Как мы уже говорили, введение иррациональных чисел определило независимость геометрии от арифметики. В книге II «Начал» Евклид геометрическим методом доказывает многие вещи, которые сегодня доказываются алгебраически, к примеру (a + b) 2= a 2+ 2ab + b 2. К этому его вынуждала проблема несоизмеримых величин, и пока не была найдена арифметическая теория, пригодная для операции с подобными числами, геометрический метод Евклида оставался для этого наиболее удобным.

√2 был первым открытым иррациональным числом, научным успехом величайшей важности, который на века определил задачи математики в области вещественных чисел. Хотя история Гиппаса, по-видимому, показывает нам величественную картину краха пифагорейской Вселенной, найти √2 несложно — сложно понять, что с ним делать. Чтобы обнаружить его, достаточно нарисовать на листе квадрат, как это сделано на рисунке 1. Главный квадрат делится на четыре маленьких со стороной 1, а затем проводятся их диагонали. Таким образом мы получаем внутренний квадрат с площадью 2, который занимает половину квадрата со стороной 2. Сторона этого внутреннего квадрата, умноженная на себя, будет равна 2. Таким образом, мы получили квадратный корень из двух, или, в современной нотации, √2. Нарисовав эту фигуру на бумаге, уже невозможно смотреть на месопотамскую табличку, хранящуюся в Йельском университете под номером YBC 7289, без некоторого изумления. Эта находка датируется периодом между 1800 и 1600 годом до н.э. и на ней изображен квадрат с двумя диагоналями, которые с легкостью позволяют найти √2. Рисунок сопровождается семью цифрами, нацарапанными клинописью по вавилонской шестидесятеричной системе. Исследователи утверждают, что эти числа соответствуют приближению √2 в первых знаках после запятой:

1 + 24/60 + 51/60 2 + 10/60 3 = 1, 41421296.

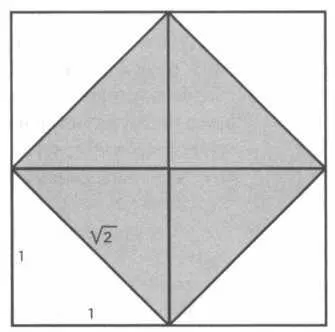
РИС. 1

Как можно увидеть на этой фотографии, исследователи смогли расшифровать клинопись на табличке YBC 7289, хранящейся в Йельском университете.

В индийском трактате «Сульвасутра» значительно более позднего времени (между 800 и 200 годом до н.э.) также можно узнать, что квадрат со стороной 1 и его диагональ не могут быть соизмеримыми. Историки математики интерпретируют следующие слова из книги как приближение √2: «...длина стороны увеличивается на треть, а эта треть на ее четвертую часть, и из этого вычитается тридцать четвертая часть этой четверти». Числовое выражение этой формулы будет таким:

√2 = 1 + 1/3 + 1/(3 · 4) - 1/(3 · 4 · 34) = 577/408 = 1, 414215686.

И все-таки, хотя подобные свидетельства весьма впечатляют, вавилоняне, индийцы и, конечно, египтяне использовали дроби исключительно в практических целях, и это положение не изменилось до развития греческой математики. Вавилоняне не знали, что их шестидесятеричные приближения никогда не будут вполне точными, так же как и египтяне не могли понять саму суть иррациональных чисел. Вопреки намерениям пифагорейцев, их заслуга состояла в открытии, что несоизмеримые соотношения — это нечто совершенно отличное от соизмеримых. Теория пропорций для несоизмеримых соотношений и для любых типов величин была впоследствии выдвинута Евдоксом Книдским (ок. 408-355 до н.э.), философом, математиком и врачом, который был учеником Платона (ок. 427-347 до н.э.).