Поясним это утверждение несколькими примерами. Сфера — пространственная фигура, которая, очевидно, полностью сходна со своим зеркальным изображением. Как круг можно рассечь бесчисленным множеством прямых линий, каждая из которых делит его на две зеркальные половинки, так и через центр сферы можно провести бесконечное число плоскостей. Если представлять себе плоскость симметрии как зеркало, то полусфера вместе со своим отражением в зеркале образует фигуру, совпадающую с исходной сферой. Представьте себе разрезанный пополам шарик для настольного тенниса. Если одну из половинок прижать к зеркалу линией разреза, то эта половинка вместе с отражением будет выглядеть как целый шарик. Сфера — не единственная трехмерная фигура, обладающая бесконечным числом плоскостей симметрии. Цилиндрическая сигарета, например, имеет бесконечное множество таких плоскостей, проходящих через ось сигареты плюс еще одна плоскость, которая проходит через центр сигареты и перпендикулярна ее оси. У конусообразного стаканчика с мороженым через ось тоже можно провести бесчисленное множество плоскостей симметрии, но плоскости симметрии, перпендикулярной оси конуса, нет. Чтобы быть симметричным, трехмерный объект должен иметь по крайней мере одну плоскость симметрии, хотя таких плоскостей он может иметь сколько угодно. У пирамиды Хеопса четыре плоскости симметрии. У кирпича — три. У стола с прямоугольной крышкой — две, а у стула или кофейной чашки только по одной. Если распилить чашку на две половинки вдоль плоскости симметрии и любую из полученных половинок прижать к зеркалу, «получится» целая чашка — в этом и заключается, конечно, смысл понятия «плоскость симметрии». Плоскость симметрии чашки наталкивает на каверзный вопрос: где у чашки ручка — слева или справа?
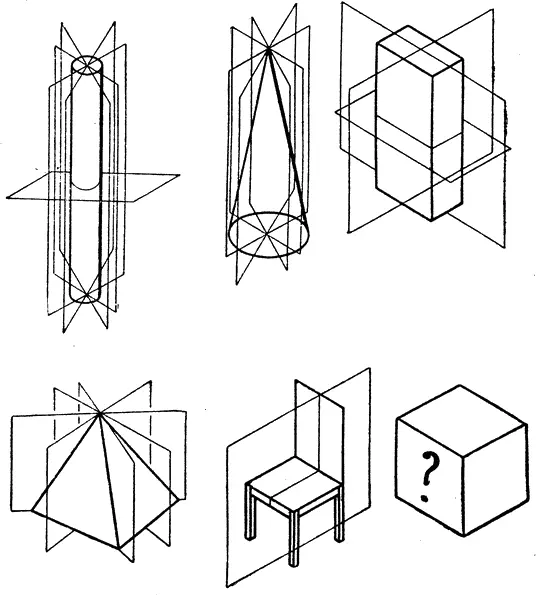
Рис. 10. Плоскости симметрии.
На рис. 10 изображены шесть трехмерных тел. У всех, кроме куба, проведены плоскости симметрии. Изучите изображение куба внимательно и попытайтесь ответить на такой вопрос:
Упражнение 2.Сколько плоскостей симметрии у куба?
Для совмещения симметричного трехмерного предмета со своим зеркальным изображением может потребоваться поворот в 3-пространстве. Предположим, вы подносите к зеркалу конический стаканчик с мороженым. Если держать его, как показано на рис. 11 слева, чтобы плоскость зеркала была параллельна одной из плоскостей симметрии конуса, то можно совместить предмет с изображением, просто сдвинув их вместе. Но если конус направлен вершиной в сторону зеркала (правая часть рис. 11), то в этом случае, как говорят, предмет и отражение будут иметь разную ориентацию в 3-пространстве. Для того чтобы совместить эти две фигуры, одну из них необходимо повернуть так, чтобы оба конуса были сориентированы одинаково. В данном случае сферу вращать никогда не придется, потому что плоскость зеркала всегда будет параллельна одной из бесчисленного множества плоскостей симметрии сферы.
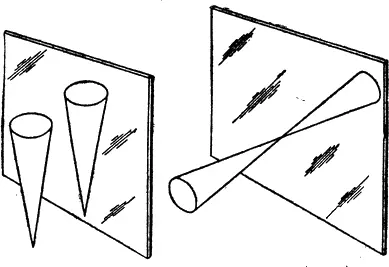
Рис. 11. Конусы можно наложить на зеркальное изображение независимо от ориентации.
У асимметричных пространственных объектов нет ни одной плоскости симметрии; их никогда нельзя совместить с отражением в зеркале независимо от ориентации — это, например, всем известные спиральная пружина и винтовая лестница. Точно так же, как спираль является асимметричной фигурой в плоскости, пружина — трехмерная спираль — асимметрична в 3-пространстве. Как ни пытайтесь, вам не удастся плоскостью рассечь пружину на две зеркально симметричные половинки. Поднесите пружину к зеркалу. Как бы вы ее ни поворачивали, в зеркале она всегда «получается не такой».
Каждая асимметричная фигура имеет зеркального двойника, который во всех деталях совпадает с ней — только «получается не такой». Две асимметричные фигуры, являющиеся зеркальным изображением одна другой, называются энантиоморфами. Каждая из них энантиоморфна другой. Знакомый пример пары энантиоморфов — ваши собственные руки. Посмотрите на них, сблизив ладони, и увидите, что одна — зеркальное отражение другой. Этот пример стал таким обыденным, что любые энантиоморфы различают, называя одни из них «правыми», а другие «левыми». Пара перчаток, ботинок или ваши уши — все это энантиоморфы.
Читать дальше














