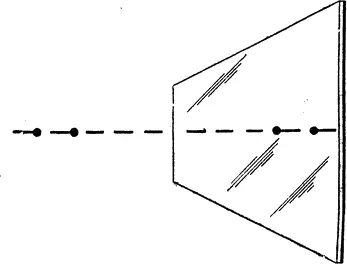
Рис. 4. Одномерцы и их зеркальные изображения.
А симметричны ли взрослые одномерцы? Нет, потому что мы не можем совмещать их с зеркальными изображениями, перемещая по прямой, — дело в том, что концы у взрослых одномерцев разные. Пусть линия, на которой они живут, простирается с востока на запад. Если взрослый одномерец обращен лицом на восток, его зеркальный двойник будет смотреть на запад. Мы, конечно, можем перевернуть одномерца и точно совместить с изображением, но для этого придется «снять» его с линии и произвести поворот в пространстве более высокой размерности — в двумерном мире. Поскольку, не выходя в пространство высшей размерности, нельзя наложить взрослого одномерца на его зеркальный образ, мы говорим, что эта фигура асимметрична.
Есть и другой способ отличить в Лайнландии симметрию от асимметрии. Если фигура симметрична, то у нее всегда есть точка (только одна) в самом центре, которая делит фигуру на две идентичные половинки, причем одна из них есть отражение другой. Такая точка называется центром симметрии. Если мы поместим зеркало перпендикулярно линии в этой точке, оставшаяся часть фигуры вместе со своим отражением будет точно воспроизводить исходную фигуру независимо от того, в какую сторону обращено зеркало. Можно ли считать тогда, что одномерец с глазами с обоих концов симметричен? Да. Такую фигуру можно было бы наложить на зеркальное изображение, и у нее был бы центр симметрии, делящий фигуру на две зеркальные половинки.
Пусть в Лайнландии живут только три взрослых одномерца — А, Б и В, причем все они «смотрят» на восток. Если мы получим зеркально обращенную картину одного из них, скажем среднего, то все трое мгновенно заметят перемену. Теперь А и Б «глядят друг на друга», а Б и В «повернуты спинами» один к другому. Но если вся прямая окажется зеркально отраженной, то есть вся «вселенная» одномерцев, то сами они о происшедшей перемене не смогут узнать. В действительности для них просто не имеет смысла говорить о какой-либо перемене. Мы знаем, что направление линии изменилось на обратное, но знаем потому, что живем в 3-пространстве и можем наблюдать положение Лайнландии по отношению к внешнему миру. Но одномерцы не могут представить себе пространство размерности большей чем единица. Они знают только свой собственный мирок, ту единственную прямую, на которой живут. С их точки зрения, никакого изменения не произошло. Только в том случае, когда операции зеркального отражения подвергается какая-то часть их «вселенной», одномерцы смогут заметить перемену.
Во Флатландии, в 2-пространстве планиметрии, все обстоит интереснее, но в отношении зеркальной симметрии предметы ведут себя практически так же, как в Лайнландии. На рис. 5 наш художник дал стилизованное изображение асимметричного двумерца и его отражения в вертикальном зеркале. (Оно изображено объемно, в 3-пространстве, но зеркало двумерца — это всего лишь прямая линия, которую он видит перед собой.) Совместить двумерца с зеркальным изображением невозможно. Если бы мы могли его взять с плоскости, как бумажного солдатика, перевернуть и снова положить в перевернутом виде, то все это можно было бы произвести в 3-пространстве, а не в 2-пространстве Флатландии. Что же произойдет, если держать зеркало над двумерцем или под ним, как показано на рис. 6? В этом случае поменяются местами верх и низ, потому что зеркало перпендикулярно вертикальной оси. Но изображение в зеркале получится таким же, как и прежде; изменится только его положение на плоскости. Мы можем взять любое из зеркальных изображений на рис. 6 и, перевернув, совместить их точка в точку с зеркальным изображением на рис. 5. Где именно помещено зеркало — не имеет ни малейшего значения, так как отражение асимметричного двумерца всегда получается одинаковым.
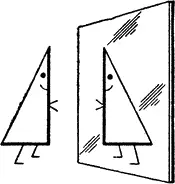
Рис. 5. Двумерец и его отражение в вертикальном зеркале.
Нетрудно изобразить разные геометрические фигуры Флатландии, которые являются симметричными и не меняются при отражении в зеркале. Квадраты, окружности, эллипсы, равносторонние и равнобедренные треугольники, значки карточных мастей — бубновой, червонной, пиковой и трефовой — все они при отражении остаются неизменными. В Лайнландии, как мы уже знаем, у каждой симметричной фигуры есть точка, которая делит фигуру на зеркальные половинки. С симметричными фигурами Флатландии то же самое делает прямая линия , называемая осью симметрии. На рис. 7 приведены примеры различных симметричных фигур на плоскости. Оси симметрии указаны пунктирными линиями. Обратите внимание на то, что у фигуры может быть разное число осей симметрии — от одной до бесконечности. Круг — единственная плоская фигура, имеющая бесконечное число таких осей. Другие фигуры могут иметь хоть и не бесконечное, но произвольно большое число подобных осей. Если поместить зеркало так, чтобы его край совпадал с осью симметрии, то оставшаяся перед зеркалом часть фигуры вместе с отражением, как и в Лайнландии, точно повторит форму исходной фигуры.
Читать дальше














