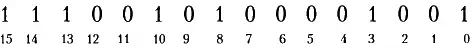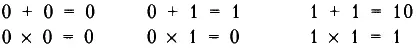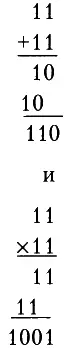Айзек Азимов - Числа - от арифметики до высшей математики

Перевод числа из двоичной системы в десятеричную не составляет труда. Рассмотрим, например, выражение 11001 в двоичной системе. Оно эквивалентно (1 × 2 4) + (1 × 2 3) + (0 × 2 2) + (0 × 2 1) + (1 × 2 0), или 16 + 8 + 0 + 0 + 1, или 25, что соответствует эквиваленту, приведенному в таблице.

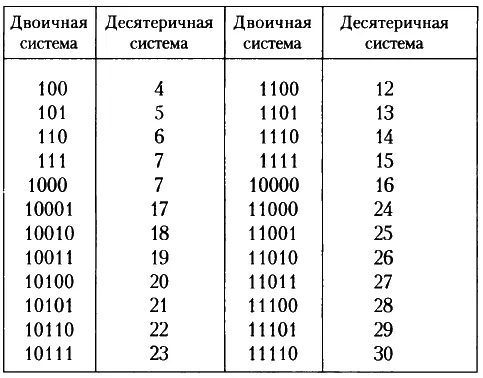
Этот процесс можно упростить, если принять во внимание, что число 2, возведенное в степень, умножается либо на 0, и тогда результат тоже будет равен нулю и его можно не учитывать, либо на 1, и тогда это просто 2, возведенное в какую-то степень.

Таким образом, мы можем проставить порядковый номер справа налево, как это показано ниже маленькими цифрами:

Каждое маленькое число — это степень числа 2, определяемая положением цифры в числе, представленном в двоичной системе. Следует учитывать только те показатели степени, которые стоят против единиц. Показатели, стоящие против нулей, можно опускать. Используя такой подход, можно записать число 11001 как 2 4+ 2 3+ 2 0, или 16 + 8 + 1, или 25.

Большие числа, такие как 1 110 010 100 001 001, можно переводить в десятеричную систему таким же образом.

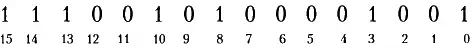
Поскольку единицам соответствуют позиции 0, 3, 8, 10, 13, 14 и 15, то число будет равняться 2 15+ 2 14+ 2 13+ 2 10+ 2 8 + 2 3+ 2 0, или 32768 + 16384 + 8192 + 1024 + 256 + 8 + 1, или 58 633.

Обратный перевод из двоичной системы в десятеричную не очень сложен, но более длителен. Предположим, число 1562 выражено в десятеричной системе. В двоичную систему его можно перевести следующим образом:

Наибольшее число, соответствующее двойке, возведенной в степень, и меньшее 1562, — это 2 10(или 1024). Если мы вычтем 1024 из 1562, у нас останется 538. Теперь наибольшее число, соответствующее двойке, возведенной в степень, и меньшее 538, — это 2 9(или 512). После вычитания этой величины из 538 у нас остается 26. Ближайшее и меньшее число теперь — 2 4(или 16). После вычитания остается 10. Теперь ближайшее число — это 2 3(или 8). После вычитания остается 2 или 2 1. Таким образом, 1562 = 2 10+ 2 9+ 2 4+ 2 3+ 2 1.

Теперь надо только правильно расставить по местам показатели степени справа налево. Единицы будут стоять на 1, 3, 4, 9 и 10-й позициях. На остальных позициях мы поставим нули. Таким образом, мы получаем число 11 000 011 010, двоичный эквивалент числа 1562 в десятеричной системе.

В двоичной системе очень простые таблицы сложения и умножения:

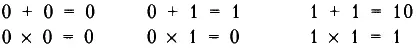
И это весь список.

Таким образом, в двоичной системе:

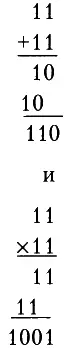
Правильность этих вычислений можно, при желании, проверить, учитывая, что числа И, 110 и 1001 в двоичной системе равны соответственно 3, 6 и 9 в десятеричной системе.

Теперь представьте себе, что у вас есть счетная электронная машина с набором переключателей (например, полупроводниковых). Каждый переключатель может находиться в одной из двух позиций — «включено» (когда ток проходит через переключатель) или «выключено» (когда ток не проходит через переключатель).

Теперь предположим, что положение «включено» соответствует 1, а положение «выключено» соответствует 0. В этом случае счетную машину можно спроектировать таким образом, чтобы переключение электрического сигнала различными переключателями подчинялось правилам сложения, умножения и другим действиям с единицами и нулями в двоичной системе.

Такая машина будет так быстро производить переключение и производить вычисления с такой скоростью, что сможет выполнить за считаные секунды такой объем вычислений, на который человеку потребовалось бы не меньше месяца.

Однако, рассматривая различные системы счета, мы сильно уклонились от основной темы нашей книги. Теперь мы возвращаемся к десятеричной системе, и вся дальнейшая информация будет подана именно в десятеричной системе.

Для того чтобы четко уяснить себе, какие действия можно производить с экспоненциальными числами на основе 10, начнем работать с относительно небольшими числами, а не с такими огромными, как масса Земли, о которой шла речь в начале главы.