Для того чтобы избежать такого несоответствия, следует вставить в ряд дискретных чисел какие-то промежуточные числа. Когда мы это сделаем, числа 1, 2, 3, 4… становятся только малой частью бесконечной системы, которая соответствует таким понятиям, как время, длина, или любому другому континууму.
Со следующей главы мы начнем изучать такие числа, выясним их происхождение и освоим правила расчетов при помощи таких чисел.
Делим единицы
Человечество не могло согласиться с ограничениями в делении. Предположим, надо разделить два яблока между четырьмя детьми. Совершенно бесполезно объяснять им, что такое деление невозможно, поскольку нет такого числа, которое после умножения на 4 даст 2. И ни одна мать так не сделает. Она попросту разрежет каждое из яблок пополам и даст каждому из детей половину (или приготовит из этих яблок пюре).
Следуя этой системе, человечество уже давно научилось разбивать основные единицы измерения на более мелкие и присваивать этим новым единицам собственные названия. Например, в американской системе измерения объема существует единица, называемая кварта, если кварту разделить пополам, получим две новые единицы, пинты. Если у вас есть две кварты пива, на которое претендуют четыре человека, то каждый получит по одной пинте.
Можно делить единицы и на числа, большие 2. Например, бушель (еще одна американская мера объема) можно разделить на 4 пека, а пек — на 8 кварт. Один фунт можно разделить на 16 унций, а 1 кварту на 32 жидкие унции. Все эти числа являются результатом деления какой-то величины на две части, затем каждую из этих частей снова делили пополам и так далее.
Можно, например, разделить 1 кварту между двумя людьми, если каждому дать по 16 жидких унций (а это как раз 1 пинта). А если надо разделить одну кварту между четырьмя людьми, то каждому можно дать по 8 жидких унций (то есть по полпинты). Если же у нас 8 человек, то каждому достанется по 4 жидкие унции (или по 1 джиллу).
Все это замечательно, но что делать, если надо разделить что-то между тремя? Мы не можем разделить кварту, в которую входят 32 унции, на три, поскольку 32 не делится на 3. Кварту удобно делить между 16 или 32.
Следовательно, было бы полезно выбрать какую-нибудь единицу, которая содержала бы максимальное количество сомножителей. Одним из таких чисел является 12. В одном футе 12 дюймов, 12 тройских унций содержится в тройском фунте, а 12 — это, как известно, дюжина.
Обратите внимание на дюжину, это очень полезная единица. Если у вас есть дюжина яблок, вы можете поделить их на две группы по 6, на 3 группы по 4, на 4 группы по 3, на 6 групп по 2, и на 12 групп по одному. Очень важно, что 12 делится не только на 2 и 4, но также и на 3.
Дюжины раньше часто использовали в торговле, ведь дюжину легко разбить на несколько более мелких частей различными путями. Существовала также единица, которая являлась дюжиной дюжин (это гросс), которая равнялась 12 × 12 или 144. У числа 144 много сомножителей. Это 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48 и 72.
Такая система удобна и практична, ее легко применять в повседневной жизни, и кое- кто даже жалеет о том, что в основе нашей системы исчисления лежит 10, а не 12. У числа 190 есть только два множителя, это 2 и 5. Десять не делится ни на 3, ни на 4. Единственная причина, по которой в основе системы оказалось число 10, — это то, что у нас по 5 пальцев на каждой руке. А вот если бы их было бы по 6…
У числа 10 есть одно преимущество перед 12. Число 10 делится на 5, а 12 — нет. Древние вавилоняне пытались соединить в одном числе все достоинства чисел 10 и 12. Такое число должно делиться не только на 2, 3, и 4, но и на 5. Наименьшим таким числом является 60. Это число используется и в астрономии. Год составляет 365 дней и несколько часов. Год — это то время, за которое Солнце совершает свой (кажущийся) круговой путь по небу относительно неподвижных звезд. Если полный круг разделить на величину пути, которое Солнце проходит за день (то есть на «путь-день»). Мы получим 365 долей круга.
У вавилонян год равнялся 360 дням (либо они неправильно вычислили продолжительность года, либо просто округлили 365 до 360 для удобства вычислений). С этим числом удобно работать, поскольку 360 — это 60 × 60. Поэтому они делили небесную сферу и другие круги на 360 равных частей, которые мы в наши дни называем градусами. Затем каждый градус они делили на 60 частей, которые мы называем минутами, а каждую минуту еще на 60 частей, на 60 секунд.
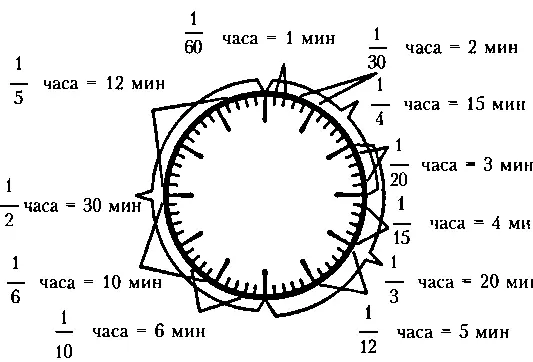
Час, состоящий из 60 минут.
Мы до сих пор придерживаемся вавилонской системы. Более того, поскольку время измеряется по движению крупных небесных тел на небосклоне, наш час разделен на 60 минут, а минута — на 60 секунд.
Читать дальше












