Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

С дифференцированием неразрывно связан обратный ему процесс – интегрирование. Интеграл от f ( x ), или ∫ f ( x ) dx , восстановит значение функции f ( x ) до ее дифференцирования. Определенный интеграл

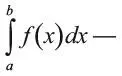
это площадь под графиком между значениями x = a и x = b .

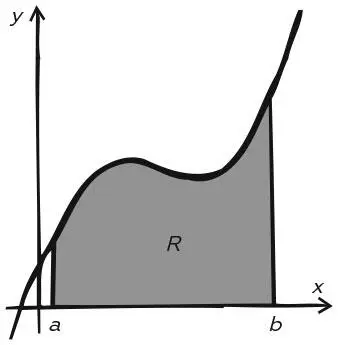
Определенный интеграл

Производные и интегралы решили проблемы, из-за которых буксовали исследования предшественников. Скорости, касательные, максимумы и минимумы можно было вычислить при помощи дифференцирования. Длины, площади и объемы поддавались вычислению с помощью интегрирования. Но и это не всё. Как ни удивительно, но оказалось, что и законы природы могут быть изложены на языке исчисления.

По мере того как росла важность исчисления для передовой науки, рос и престиж ученого, стоявшего у ее истоков. Но кто был этим ученым?

Как мы видим, Ньютон стал задумываться над исчислением примерно с 1665 г., хотя ничего не публиковал на эту тему до 1687 г. Лейбниц, чьи идеи развивались примерно тем же путем, что и у Ньютона, начал исследовать исчисление в 1673 г. и первые труды в этой области издал в 1684 г. Оба работали независимо, но Лейбниц мог узнать о трудах Ньютона, когда побывал в Париже в 1672 г. и в Лондоне в 1673 г. В 1669 г. Ньютон отослал копию «Анализа» Барроу, а Лейбниц встречался со многими людьми, также знавшими Барроу и, возможно, имевшими представление об этой работе.

Когда Лейбниц опубликовал свою книгу в 1684 г., кое-кто из окружения Ньютона ужасно возмутился – вероятно, потому, что Ньютона опередили с публикацией прямо перед финишной чертой. Все они с запозданием осознали, что было поставлено на кон, – и дружно обвинили Лейбница в краже идей Ньютона.

Примером ранних попыток использовать исчисление для описания явлений природы можно считать вопрос о подвешенной цепи. Ответ всегда оставался спорным: одни ученые утверждали, что это парабола, а другие не соглашались. В 1691 г. Лейбниц, Кристиан Гюйгенс и Иоганн Бернулли опубликовали предполагаемые решения. Самое удовлетворительное принадлежало Бернулли. Для описания положения цепи он использовал дифференциальное уравнение, исходя из ньютоновой механики и законов движения. Как показало это уравнение, решением стала не парабола, а кривая, известная теперь под названием цепная линия , с уравнением:

y = k ( e x + e −x ),

где k – константа.

Подвешенная цепь является графиком цепной линии

Зато несущие цепи на подвесных мостах имеют форму параболы. Эта разница возникает оттого, что цепи несут на себе и вес моста, и собственный. И снова это можно показать при помощи исчисления.

Клифтонский подвесной мост – парабола

Математики на континенте, особенно братья Бернулли, грудью встали на защиту Лейбница, полагая, что именно Ньютон был замешан в плагиате. На самом деле оба сделали свои открытия почти независимо друг от друга, как показали их неопубликованные рукописи. Добавило туману и то, что оба во многом опирались на предыдущую работу Барроу, который, вероятно, имел больше оснований для жалоб, чем любой из них.

Обвинения могли быть легко сняты, но вместо этого спор стал более ожесточенным; Иоганн Бернулли перенес свою неприязнь к Ньютону на всех англичан. Результатом стала катастрофа английской математики: англичане застряли в ньютоновском геометрическим стиле мышления, который сложно было использовать, а математики с континента использовали более формальный алгебраический метод и продвигали исчисление вперед быстрыми темпами. Поэтому большая часть заслуг в математической физике ушла к французам, немцам, швейцарцам и голландцам, а английская математика томилась в тихой заводи.

Важнейшей идеей, порожденной изобилием трудов об исчислении, стало существование и использование принципиально нового типа уравнений – дифференциальных уравнений . Алгебраические уравнения описывают неизвестную величину с разными степенями. Дифференциальные же гораздо более изощренны: они описывают различные производные от неизвестной функции .