Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

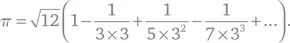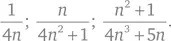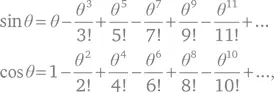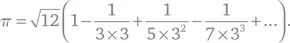
Он вычислил первый 21 член ряда и получил π с точностью до 11 знаков после запятой. Этот ряд стал первым новым методом вычисления π после Архимеда, использовавшего все более близкие по форме к окружности правильные многоугольники.

Один из приемов Мадхавы удивительно хитроумен. Мадхава оценил ошибку, возникающую при усечении ряда на некотором конечном этапе. Мало того, он привел три выражения для ошибки, которые можно прибавлять к общему значению в качестве корректирующего члена для повышения точности. Вот его выражения для ошибки после сложения n членов ряда:

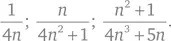
Третье из этих выражений он использовал для получения улучшенного значения суммы при расчете π с точностью до 13 знаков после запятой. Ничего подобного не наблюдается нигде в математической литературе до нынешних времен.

В 1676 г. Ньютон написал письмо Генри Олденбургу – секретарю Королевского общества; в письме он информировал этого достойного человека о двух бесконечных рядах для синуса и косинуса:

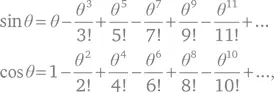
которые он вывел кружным путем, с использованием дифференциального исчисления. Сегодня мы знаем, что эти выражения, долгое время приписывавшиеся Ньютону, были получены Мадхавой почти на 400 лет раньше. Подробности вывода этих рядов приведены в «Юктибхасе». Метод вывода сложен, но его можно рассматривать как ранний вариант метода интегрального исчисления – суммирование подобных рядов член за членом.

В самом деле, утверждается, что Мадхава выработал некоторые базовые понятия дифференциального и интегрального исчисления задолго до Ньютона. Речь идет о дифференцировании, интеграле как площади под кривой и почленном интегрировании. Он нашел методы разложения многочленов в алгебре, вывел числовой метод решения уравнений посредством итераций и работал над бесконечными цепными дробями.

Джозеф спрашивает, могли ли идеи Мадхавы просочиться в Европу. Он указывает, что европейские исследователи, такие как Васко да Гама, хорошо знали Кералу, потому что это удобный остановочный пункт для кораблей, пересекающих Аравийское море на пути в Китай и другие страны Востока. Роль этого региона как центра торговли восходит еще к вавилонским временам. Географическая изоляция, зажатость между Западными Гатами и Аравийским морем, защищала его от бурной политической жизни остальной части средневековой Индии, что было дополнительным бонусом для чужеземных путешественников. Действительно, создается впечатление, что кое-что из достижений керальской техники и местных изделий в то время добиралось до Европы, однако до сих пор не найдено никаких свидетельств прямого переноса математических идей. Так что до тех пор, пока на свет не появятся новые свидетельства (если появятся), нам остается предполагать, что Керала и Европа открыли множество важных математических идей независимо друг от друга.

Работа таких выдающихся индийских математиков, как Ариабхата и Брахмагупта, давно признана в Европе. С трудами Керальской школы европейское научное сообщество впервые познакомилось только в 1835 г., когда Чарльз Виш написал статью о четырех самых значительных индийских текстах: это «Тантрасамграха» Нилаканты, «Юктибхаса» Естхадевы, «Карана Паддхати» Путхуманы Сомайаджи и «Садратнамала» Санкары Вармана. Виш, можно сказать, запустил лису в курятник, когда заявил, что «Тантрасамграха» содержит основы работы с производными, как Ньютон называл дифференциальное исчисление (глава 7): что в ней «полно производных форм и рядов, которые невозможно найти ни в одном труде других стран». В дни, когда всю торговлю с Индией контролировала Ост-Индская компания, а сама страна рассматривалась как легкая добыча для завоевателя, это заявление не произвело совершенно никакого впечатления. Керальская математика была быстро и прочно забыта. Только столетие спустя, в 1940-х гг., ее высокий уровень был наконец вновь описан в серии статей Кадамбура Раджагопала и его соавторов; они проанализировали математику Керальской школы и продемонстрировали, что индийские математики открыли множество важных вещей намного раньше европейцев, которым эти достижения, как правило, приписывали.