Георгий Гамов - Занимательная математика

— Действительно, кажется, я понял, как решить задачу, — сказал Стерн. Фон Карман делит сливовицу на три порции, которые он считает равными, и поэтому будет удовлетворен, получив любую из них.

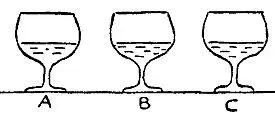
Если Гамов считает, что в рюмке А сливовицы больше, чем в В или С, а я считаю, что больше всего сливовицы налито в рюмку В, то никаких осложнений не возникает. Гамов берет себе рюмку А, я — рюмку В, а фон Карман получает рюмку С. Затруднение может возникнуть только в том случае, если и Гамов, и я сочтем, что больше всего сливовицы оказалось налитой в рюмку А. Но и в этом случае, если мы оба согласимся, что в рюмке В сливовицы больше, чем в рюмке С, то задача существенно упрощается. Гамову и мне необходимо разделить содержимое рюмок В и С так, как это делают двое детей в задаче о честном разделе, а фон Карману достанется рюмка С.

Единственная трудность возникает в том случае, когда и Гамов и я сочтем, что больше всего сливовицы в рюмке А, но при этом Гамову будет казаться, что в рюмке В сливовицы больше, чем в рюмке С, а мне — что в рюмке С сливовицы больше, чем в рюмке В. В этом случае я предоставлю Гамову разделить содержимое рюмок А и В так, как ему кажется будет поровну. При этом он перельет часть сливовицы из рюмки А в рюмку В.

Если после переливания я буду по-прежнему думать, что в рюмке А сливовицы больше, чем в любой из двух остальных рюмок, и возьму ее себе, то Гамову не останется ничего другого, как выбрать рюмку В, поскольку до переливания он считал, что меньше всего сливовицы в рюмке С, а это означает, что в С заведомо меньше 1/3 всей сливовицы.

Разумеется, фон Карман предпочел бы выбрать рюмку В, так как после того, как он разлил поровну (как ему казалось) сливовицу по трем рюмкам, Гамов добавил в В сливовицы из рюмки А. Но поскольку задача сформулирована так, что каждый из нас должен быть удовлетворен, если получит по крайней мере причитающуюся ему долю спиртного, т. е. 1/3 всей сливовицы, фон Карман не сможет протестовать, даже если Гамов выберет рюмку В.

Если же после того, как Гамов отольет сливовицу из рюмки А в рюмку В, то в силу тех же соображений я бы выбрал рюмку В. Гамов довольствовался бы рюмкой А, а фон Карману досталась бы рюмка С.

Если бы после переливания я решил выбрать рюмку С, то фон Карман мог бы взять рюмку В, а Гамов должен был бы взять рюмку А.

Выслушав решение, фон Карман улыбнулся:

— Теперь вы понимаете, почему я слегка изменил условия задачи?

Вместо того чтобы каждый из нас считал себя удовлетворенным, если ему досталось по крайней мере столько же сливовицы, сколько любому из остальных, я предложил, чтобы каждый из нас довольствовался, получив не менее причитающейся ему честной доли 1/3 сливовицы.

Один из этапов вашего решения показывает, что задача в первоначальной формулировке неразрешима.

Эту головоломку, мне кажется, можно по праву отнести к проблемам с моралью из области человеческих отношений.

Принятые в Квазиабабии торговые единицы веса воспроизводят систему единиц, имевших хождение в Англии, США и Странах Содружества до введения метрической системы. В 1 торговом фунте 16 унций (453,59 г). В 1 унции 28,35 г. (Унция делилась на 16 драхм {по 1,77 г), драхма — на 3 скрупулы (по 0,59 г) и скрупула — на 10 гран (но 0,059 г)). — Прим. перев.

Великий султан предполагает в своих рассуждениях, что соотношение мальчиков и девочек равно. Это не вполне корректно с точки зрения биологии. — Прим. авт .

Сюжет этой истории сообщил одному из нас (Г. Г.) проф. Виктор Амазаспович Абмарцумян. (Академик В. А. Амбарцумян — выдающийся астрофизик. — Прим. перев .)

Сюжет этой истории сообщил одному из нас (Г. Г.) проф. Альберт Сент-Дьерди.

(Известный биохимик, один из основоположников биоэнергетики. — Прим. перев .)

В предлагаемом варианте объяснение непосредственно применимо и к задаче о лифтах, о которой шла речь в прологе.

Так как для рассуждения важны не абсолютные, а относительные расстояния, единицы длины не существенны (при условии, что оба расстояния измеряются в одних и тех же единицах). — Прим. перев .

Задачу можно решать и в милях, не переводя их в привычные километры. Для тех читателей, кто захочет «ощутить» полученный ответ, сообщаем, что 1 миля = 1609.315 метра. (Это так называемая английская («сухопутная») миля. Ее не нужно смешивать с более длинной морской милей (1852 м).) — Прим. перев .