Единственные функции, кроме логарифма, производные которых нам понадобятся в этой книге, — это простые степенные функции x N . Приведем без доказательства тот факт, что для любого числа N производная функции x N есть функция Nx N−1. Таблица 7.1 дает некоторые производные степенных функций.
| Функция |
Производная |
| x −3 |
−3 x −4 |
| x −2 |
−2 x −3 |
| x −1 |
− x −2 |
| x 0 |
0 |
| x 1 |
1 |
| x 2 |
2 x |
| x 3 |
3 x 2 |
Таблица 7.1.Производные функций x N .
Конечно, x 0— это просто единица, а график этой функции — горизонтальная прямая. У нее нет наклона — точнее, нулевой наклон. Дифференцирование любого фиксированного числа дает нуль. А x 1— это просто x , график же представляет собой прямую, идущую по диагонали вверх и покидающую рисунок через правый верхний угол. Наклон ее повсюду равен 1. Заметим, что нет такой степенной функции, производная которой была бы равна x −1, хотя x 0вроде бы стоит на правильном месте, чтобы дать такую производную. Это неудивительно, поскольку мы уже знаем, что производная ln x есть как раз x −1. Это еще одно свидетельство того, что ln x как будто пытается выдать себя за x 0.
VII.
Вы, должно быть, помните мои слова о том, что математики обожают все обращать. Если задано выражение P через Q , то как выразить Q через P ? Именно так мы исходно и получили логарифмическую функцию — как обращение показательной функции. Если a = e b , тот как найти b через a ? Как ln а .
Так вот, предположим, что мы продифференцировали функцию f и получили функцию g. То есть g представляет собой производную функции f. А f представляет собой… (что именно?!) функции g ? В чем состоит обращение дифференцирования? Производная ln x — это 1/ x , так что ln x — это… (что?) функции 1/ x ? Ответ: интеграл, вот что. Обращение производной — это интеграл, а обращение дифференцирования — это интегрирование . Поскольку вся эта деятельность прозрачна для умножения на фиксированное число, переворачивание таблицы 7.1 вверх ногами и некоторая ее «доводка» дадут нам обратную операцию, которая и представлена в таблице 7.2. И вообще, если только N не равно −1, то интеграл от функции x N равен x N+ 1 /(N + 1 ). (Взгляд на таблицу еще раз показывает, как функция ln x изо всех сил старается вести себя как функция x 0, каковой она, конечно, не является).
| Функция |
Интеграл |
| x −3 |
− 1/ 2 x −2 |
| x −2 |
− x −1 |
| x −1 |
ln x |
| x 0 |
x |
| x 1 |
1/ 2 x 2 |
| x 2 |
1/ 3 x 3 |
| x 3 |
1/ 4 x 4 |
Таблица 7.2.Интегралы функций x N .
Если производные годятся для того, чтобы выражать наклон функции — т.е. скорость, с которой функция изменяется в данной точке, — то для чего же годятся интегралы? Ответ: для нахождения площадей под графиками.
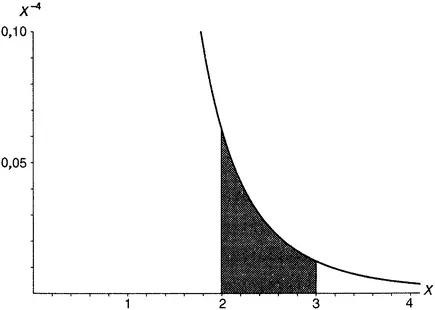
Рисунок 7.3.Для чего пригодно интегрирование.
Функция, показанная на рисунке 7.3, а это в действительности функция 1/ x 4, т.е., другими словами, x −4, — ограничивает собой некоторую площадь между аргументами x = 2 и x = 3. Чтобы найти эту площадь, сначала надо найти интеграл от x −4. Согласно приведенному выше общему правилу, этот интеграл равен − 1/ 3 x −3, т.е. −1/(3 x 3). Эта функция, как и всякая другая, имеет значение для каждого x из своей области определения. Чтобы найти площадь между аргументами 2 и 3, надо вычислить значение интеграла при аргументе 3, затем вычислить значение интеграла при аргументе 2, а потом вычесть второе значение из первого.
При x = 3 значение функции −1/(3 x 3) равно − 1/ 81, при x = 2 оно составляет − 1/ 24. Вычитаем, не забывая, что вычесть отрицательное число — это все равно что прибавить соответствующее положительное: − 1/ 81− (− 1/ 24) = 1/ 24− 1/ 81, что равно 19/ 648, т.е. примерно 0,029321.
У математиков есть специальный способ для записи всей этой процедуры: 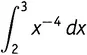 , что читается как «интеграл от икс в минус четвертой степени по дэ-икс от двух до трех». (Не слишком озадачивайтесь этим самым «по dх » — назначение этих слов состоит в указании, что именно x является основной переменной, с которой мы работаем, и именно ее интеграл надо найти. Если под знаком интеграла окажутся еще другие переменные, то они будут там присутствовать праздно, интегрирование ведется не по ним. В главе 19 у нас появится такой пример.)
, что читается как «интеграл от икс в минус четвертой степени по дэ-икс от двух до трех». (Не слишком озадачивайтесь этим самым «по dх » — назначение этих слов состоит в указании, что именно x является основной переменной, с которой мы работаем, и именно ее интеграл надо найти. Если под знаком интеграла окажутся еще другие переменные, то они будут там присутствовать праздно, интегрирование ведется не по ним. В главе 19 у нас появится такой пример.)
Читать дальше


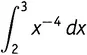 , что читается как «интеграл от икс в минус четвертой степени по дэ-икс от двух до трех». (Не слишком озадачивайтесь этим самым «по dх » — назначение этих слов состоит в указании, что именно x является основной переменной, с которой мы работаем, и именно ее интеграл надо найти. Если под знаком интеграла окажутся еще другие переменные, то они будут там присутствовать праздно, интегрирование ведется не по ним. В главе 19 у нас появится такой пример.)
, что читается как «интеграл от икс в минус четвертой степени по дэ-икс от двух до трех». (Не слишком озадачивайтесь этим самым «по dх » — назначение этих слов состоит в указании, что именно x является основной переменной, с которой мы работаем, и именно ее интеграл надо найти. Если под знаком интеграла окажутся еще другие переменные, то они будут там присутствовать праздно, интегрирование ведется не по ним. В главе 19 у нас появится такой пример.)










