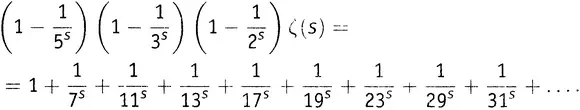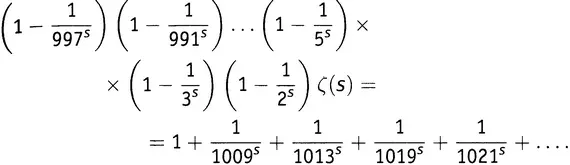Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Здесь есть возможность читать онлайн «Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.» весь текст электронной книги совершенно бесплатно (целиком полную версию без сокращений). В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Город: Москва, Год выпуска: 2010, ISBN: 2010, Издательство: Астрель: CORPUS, Жанр: Математика, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
- Автор:
- Издательство:Астрель: CORPUS
- Жанр:
- Год:2010
- Город:Москва
- ISBN:978-5-271-25422-2
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

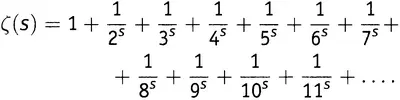
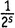 . Получим
. Получим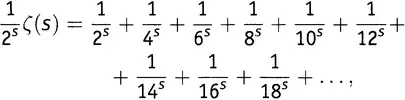
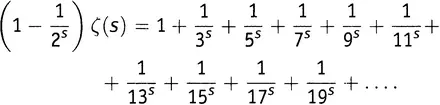
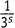 , руководствуясь тем, что 3 — это первое выжившее число в правой части:
, руководствуясь тем, что 3 — это первое выжившее число в правой части: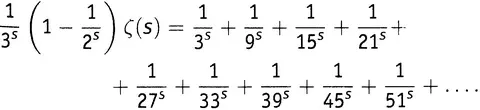
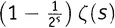 как неделимую штуку, — просто как некоторое число (каковым оно, конечно, и является при любом заданном s ). Вся эта штука входит в левую часть одного выражения с множителем 1, а в левую часть другого — с множителем
как неделимую штуку, — просто как некоторое число (каковым оно, конечно, и является при любом заданном s ). Вся эта штука входит в левую часть одного выражения с множителем 1, а в левую часть другого — с множителем 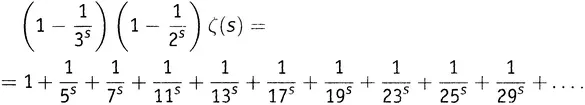
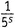 , будем иметь
, будем иметь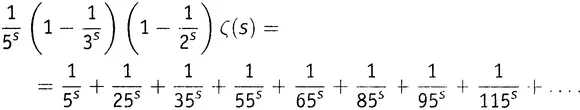
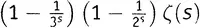 как неделимую конструкцию, видим, что в левую часть одного выражения она входит с множителем 1, а в левую часть другого — с множителем
как неделимую конструкцию, видим, что в левую часть одного выражения она входит с множителем 1, а в левую часть другого — с множителем