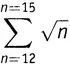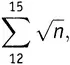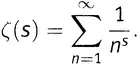Итак, к середине XVIII века немало математиков задумывались над бесконечным рядом из выражения (5.1). Точные значения — замкнутый вид — были известны для всех четных чисел N , тогда как для нечетных можно было получать приближенные значения, беря сумму достаточного числа членов. Не будем забывать, что, когда N равно 1, соответствующий ряд становится просто гармоническим рядом, который расходится. В таблице 5.1 приведены значения выражения (5.1)(которое, напомним, есть 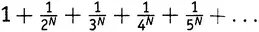 ) с точностью до 12 знаков после запятой.
) с точностью до 12 знаков после запятой.
| N |
Значение выражения (5.1) |
| 1 |
(нет значения) |
| 2 |
1,644934066848 |
| 3 |
1,202056903159 |
| 4 |
1,082323233711 |
| 5 |
1,036927755143 |
| 6 |
1,017343061984 |
Таблица 5.1.
Эта таблица похожа на один из тех «мгновенных снимков» некоторой функции, которые мы рассматривали в главе 3.iv. Так примерно дело и обстоит. Вспомним утверждение Гипотезы Римана, приведенное во вступлении.
Гипотеза Римана
Все нетривиальные нули дзета-функции имеют вещественную часть, равную одной второй.
Таблица 5.1 дает нам первое представление о дзета-функции Римана и тем самым представляет собой первый шаг к пониманию Гипотезы Римана.
VII.
Коль скоро в предшествующих разделах данной главы мы потрудились придать смысл степенной функции x a для любого числа a , а не просто для целых чисел, сейчас нет причины ограничивать букву N в выражении (5.1)целыми числами. Можно представить себе, как это число свободно парит, принимая различные значения — дробные, отрицательные и иррациональные. Нет, правда, гарантии, что ряд будет сходиться для всех чисел — как мы уже знаем из главы 1.iii, он не сходится при N = 1. Но можно, по крайней мере, попытать счастья, исследуя разные возможности.
В связи с осознанием этой новой мысли, сменим обозначение N на другую букву, которая имеет меньше традиционных ассоциаций с целыми числами. Очевидным выбором, конечно, была бы буква x . Но Риман в своей работе 1859 года не использовал икса. Подобные вопросы в его время не были урегулированы. Вместо этого он пользовался буквой s ; а его работа 1859 года приобрела такое значение, что все математики, жившие после Римана, вслед за ним использовали ту же букву. В исследованиях, посвященных дзета-функции, аргумент всегда обозначается буквой s .
И вот наконец перед нами дзета-функция Римана (дзета, которая пишется как ζ , — это шестая буква греческого алфавита) (5.2):
VIII.
Прежде чем двигаться дальше, давайте введем полезные математические обозначения, которые сократят работу по набору формул. (Думаете, легко вставить штуки, подобные выражению (5.2), в Microsoft Word?)
Если математики хотят сложить некоторое множество членов, которые все построены по общему закону, то они используют знак ∑. Это заглавная буква «сигма», восемнадцатая буква греческого алфавита, обозначающая греческую «с» (первую букву в слове «сумма»). Применяется она следующим образом. Суммируемый член, записанный с помощью данного правила, помещается «под» (на самом деле имеется в виду — справа, хотя вопреки логике говорится «под») знаком сигмы. А снизу и сверху от сигмы указывается, где сумма начинается и где заканчивается. Например, выражение
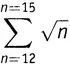
представляет собой математическую «стенографию» — краткую запись выражения √12 + √13 + √14 + √15. Сигма говорит нам: «Сложить их!»; выражения сверху и снизу от сигмы показывают, где начать сложение и где его закончить; и наконец, выражение под знаком сигмы говорит, что, собственно, надо складывать — в данном случае √n .
Математики не особенно педантичны по поводу стиля таких выражений. Приведенную выше сумму часто записывают как
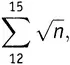
поскольку ясно, что именно n пробегает значения от 12 до 15. Теперь, вовсю используя знак сигмы, мы можем не тратить силы на лишние символы, а записать выражение (5.2)в виде
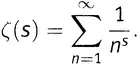
А с учетом 5-го правила действий со степенями это же можно записать как
Читать дальше

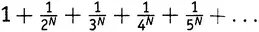 ) с точностью до 12 знаков после запятой.
) с точностью до 12 знаков после запятой.