Начав с последнего, заметим, что если x 0вообще что-нибудь будет означать, то хорошо бы добиться согласованности с теми правилами, которые у нас уже есть, потому что они являются прямым выражением здравого смысла. Возьмем во 2-м правиле n равным m. Тогда в правой части, как видно, получится x 0. А в левой части будет x m: x m. Но когда число делится само на себя, получается единица.
4- e правило действий со степенями:
x 0= 1 для всякого положительного числа x .
2-е правило можно использовать и для того, чтобы придать смысл отрицательным степеням. Разделим 12 3на 12 5. Согласно 2-му правилу, ответ должен быть равен 12 − 2. Но при этом он равен и (12×12×12)/(12×12×12×12×12), что после сокращения трех множителей 12 в числителе и знаменателе даст 1/12 2.
5-е правило действий со степенями:
x −n= 1 /x n (в частности, x − 1= 1/ x ).
3-е правило наводит нас на мысль о том, что же должны означать дробные степени. Как можно поступить с величиной x 1/3? Например, возвести ее в куб, тогда по 3-му правилу должно получиться просто x . Значит, x 1/3есть просто кубический корень из x . (Определение «кубического корня из x »: это число, куб которого равен x ). 3-е правило теперь говорит нам, какой смысл имеет всякая дробная степень; x 2/3— это кубический корень из x , возведенный в квадрат (или, что одно и то же, кубический корень из x 2).
6-е правило действий со степенями:
х m/n есть корень n- й степени из х m .
Поскольку 12 — это 3×4, получаем, что 12 5равно (3×4)×(3×4)×(3×4)×(3×4)×(3×4). Это можно переписать как (3×3×3×3×3)×(4×4×4×4×4). Короче говоря: 12 5= 3 5×4 5. Такое верно и в общем случае:
7-е правило действий со степенями:
(x×y) n = x n×y n .
А что насчет возведения x в иррациональную степень? Что могло бы означать 12 √2, или 12 π , или 12 e ? Здесь мы снова попадаем в царство анализа. Вспомним про ту последовательность из главы 1.vii, которая сходилась к √2. Она выглядела так: 1/ 1, 3/ 2, 7/ 5, 17/ 12, 41/ 29, 99/ 70, 239/ 169, 577/ 408, 1393/ 985, 3363/ 2378, … Продолжая эту последовательность достаточно далеко, можно подобраться к √2 сколь угодно близко. А из 6-го правила, которое говорит о значении всякой дробной степени, понятно, что же представляет собой число 12, возведенное в каждую из этих дробных степеней. Разумеется, число 12 1равно просто 12, а 12 3/2— это квадратный корень из 12 в кубе; 41,569219381…. Далее, 12 7/5— это корень пятой степени из 12 в седьмой степени, что равно 32,423040924…. Таким же образом, 12 17/12равно 33,794038815…, 12 41/29равно 33,553590738…, 12 99/70равно 33,594688567… и т.д. Как мы видим, эти дробные степени числа 12 сходятся к некоторому числу — на самом деле к числу 33,588665890…. Поскольку сами дроби при этом сходятся к √2, очень похоже на правду, что 12 √2= 33,588665890….
Итак, задавшись положительным числом x , можно возводить его вообще в любую степень — положительную, отрицательную, дробную или иррациональную. При этом будут выполняться приведенные выше правила действий со степенями, поскольку мы ввели определения таким образом, чтобы именно это и гарантировать! На рисунке 5.1 показаны графики функций x a для различных чисел a в интервале от −2 до 8. Отдельно отметим нулевую степень х 0, представляющую собой горизонтальную прямую на высоте 1 над осью x — то, что математики называют «постоянной функцией» (а медсестры в реанимации называют «остановкой»). Для любого аргумента x значение этой функции равно 1. Стоит еще обратить внимание, как быстро возрастают целочисленные степени x 2, x 3, x 8, а также — что имеет более прямую связь с главной темой этой книги — как медленно возрастают дробные положительные степени, такие как x 0,5.
Рисунок 5.1.Степенные функции x a для различных чисел a.
III.
Возведение чисел в степени на первый взгляд выглядит похожим на умножение. Умножение сначала представляют как кратное сложение: 12×5 = 12 + 12 + 12 + 12 + 12, затем на следующем уровне сложности объясняется, что такое 12×5 1/ 2где на самом деле содержится кое-что еще, кроме кратного умножения. Похожим образом обстоит дело и с возведением в степень. Определить 12 5совсем легко, это кратное умножение: 12×12×12×12×12. Чтобы справиться с 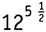 , требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
, требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
Как я уже говорил, математики обожают обращать выражения. Скажем, пусть задано выражение величины P через Q . Отлично, давайте посмотрим, можно ли выразить Q через P . И здесь аналогия между умножением и возведением в степень нарушается. Обратить умножение легко: если x = a×b, то a = x:b и b = x:a. Деление полностью решает проблему обращения умножения.
Читать дальше

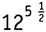 , требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
, требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.










