Генри Дьюдени - Пятьсот двадцать головоломок

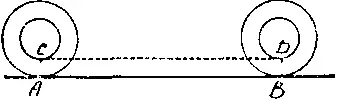
Теперь заметим, что внутренний круг (ступица) тоже делает полный оборот вдоль воображаемой пунктирной линии CD , а так как CD равно АВ , длины меньшей и большей окружностей равны! Разумеется, даже младенцу с первого взгляда ясно, что это не верно. И все же, где именно допущена ошибка?

Попытайтесь ее найти. Не может быть и тени сомнения в том, что ступица за один полный оборот проходит расстояние от С до D . Тогда почему же CD не равно длине ее окружности?

291. Знаменитый парадокс.Есть такой вопрос, который задают постоянно, но на который я никогда не слышал удовлетворительного или достаточно убедительного для неискушенного человека ответа. Он состоит в следующем: «Движется ли на ходу верхняя часть велосипедного колеса быстрее нижней?»

Люди, не привыкшие к точному мышлению, неизменно встречают такой вопрос смехом и отвечают: «Разумеется, нет!» Они считают подобный вопрос совершенно нелепым и не достойным даже того, чтобы всерьез над ним призадуматься. «Колесо, —говорят они, — это твердое тело, вращающееся вокруг центральной оси, и если одна из его частей стала бы двигаться быстрее другой, то оно разлетелось бы вдребезги».

Тогда вы обращаете внимание .вашего скептика на проезжающий мимо экипаж и просите его заметить, что спицы в нижней части колеса ясно видны, их даже можно пересчитать; а вот в верхней части они движутся так быстро, что становятся неразличимыми. Движущееся колесо выглядит примерно так, как оно изображено на рисунке. Наш друг вынужден признать очевидное, но поскольку он не может дать объяснение тому, что видит, и не хочет отказываться от своей прежней точки зрения, то, вероятно, ответит: «Ну, возможно, это обман зрения».

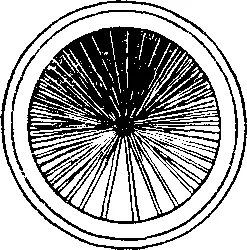
Итак, повторяем вопрос: «Движется ли верхняя часть колеса быстрее нижней?»

292. Еще один парадокс с колесом.Два велосипедиста остановились на железнодорожном мосту где-то в Сассексе, когда мимо них проходил поезд.

— Этот поезд идет из Лондона в Брайтон, — сказал Хендерсон.

— Большая его часть, — заметил Бэнкс, — а остальная — движется по направлению к Лондону.

— О чем это, скажи на милость, ты говоришь?

— Я говорю, что если поезд идет из Лондона в Брайтон, то часть этого поезда все время движется в противоположном направлении — из Брайтона в Лондон.

— И ты всерьез утверждаешь, что, когда я еду из Кройдона в Истбурн, то часть моего велосипеда несется назад в Кройдон?

— Не горячись, старина, — сказал спокойно Бэнкс. — Я ничего не говорил о велосипедах. Мое утверждение касалось только железнодорожных поездов.

Хендерсон решил, что это просто шутка и речь идет о дыме или паре, но его приятель заметил, что сильный ветер может быть и в направлении движения поезда. Тогда он высказал предположение, что имелись в виду мысли пассажиров, но проверить этого не удалось и, кроме того, вряд ли их можно было назвать частью поезда! Наконец Хендерсон сдался.

Не смог бы читатель объяснить этот любопытный парадокс?

293. Механический парадокс.Знаменитый механический парадокс, придуманный Джеймсом Фергюсоном [17] Дж. Фергюсон — шотландский астроном-самоучка XVIII в. где-то около 1751 г., следовало бы знать каждому. Он предложил его скептику-часовщику в момент спора.

— Предположим, — сказал Фергюсон, — что я сделаю одно колесо толщиной в три других и на всех их нарежу зубцы. Затем я свободно надену три колеса на одну ось и помещу толстое колесо так, чтобы оно приводило их в движение и его зубцы входили в зубцы трех тонких колес. Если я поверну толстое колесо, то как повернутся тонкие колеса?

Часовщик ответил, что, очевидно, три колеса повернутся в противоположном направлении. Тогда Фергюсон смастерил простой механизм, который под силу сделать каждому, и показал, что при вращении толстого колеса в любом направлении одно из тонких колес вращается в том же самом направлении , другое — в противоположном , а третье остается неподвижным . Хотя часовщик и взял механизм домой, он так и не смог найти объяснение этому странному парадоксу.

294. Четыре домовладельца.Вы видите на рисунке квадратный участок земли с четырьмя домами, четырьмя деревьями, колодцем ( W ) в центре, а также изгородями с четырьмя калитками ( G ).