Сэм Лойд - Самые знаменитые головоломки мира

180.Два кувшина уравновешиваются тремя блюдцами, так что вес одного блюдца равен 2/3 веса кувшина. Теперь добавим на каждую чашу весов второго рисунка по стакану; при этом в левой чаше окажутся те же предметы, что и в левой чаше первого рисунка. Это означает, что вес кувшина равен весу блюдца и двух стаканов, а поскольку вес блюдца равен 2/3 веса кувшина, то вес двух стаканов равен оставшейся 1/3 Следовательно, вес каждого стакана равен 1/6 веса кувшина.

На первом рисунке мы видим, что стакан (1/6 веса кувшина) и бутылка уравновешивают кувшин; отсюда мы находим, что вес бутылки составляет 5/6 веса кувшина. Таким образом, чтобы уравновесить бутылку на последнем рисунке, требуется 5 стаканов.

181. Дополнительное количество спиртного, купленное агентом, увеличило стоимость всего запаса до 343 долларов. К этой сумме он сделал надбавку в 10 %, что привело к общей продажной стоимости, равной 377,3 доллара. Агент продал спиртного на 285,8 доллара, а на руках у него осталось напитков на 91,5 доллара, как и показано на рисунке. Стоимость этого остатка без 10 %-й надбавки составляет 83,18 доллара. Вычитая ее из 343 долларов (общей стоимости спиртного), мы находим стоимость проданного спиртного – 259,82 доллара. Мы вычитаем это значение из общей продажной стоимости в 285,8 доллара и находим, что доход города на продаже спиртного составил 25,98 доллара.

Это можно проверить следующим образом. Доход в 25,98 доллара плюс аванс в 12 долларов и 59,5 доллара стоимости напитков дают в сумме 97,48 доллара. Отсюда мы вычитаем комиссионные агента, равные 14,29 доллара, что дает стоимость оставшегося спиртного в 83,19 доллара и показывает, что расчеты агента были правильными в пределах 2 центов.

182. У леди в начале прогулки было 42 цента.

183. Дети были настолько не в ладах с календарем, что отправились в школу воскресным утром!

184.[Пусть х означает общее число столбов, а у – число часов, за которое автомобиль проезжает 3 5/8 мили. Автомобиль минует х столбов за у часов, то есть х/у столбов в час, или х /60 у столбов в минуту. Поскольку нам известно, что число столбов, мимо которых автомобиль проезжает за минуту, умноженное на 3 5/8, равно его скорости, выраженной в милях в час, мы можем составить следующее уравнение: 3 5/ 8 х / 60у = 3 5/ 8 / у.

Произведя сокращение на общий множитель в левой и правой частях, мы находим, что х = 60.

Поскольку линия длиной в 3 5/8 мили, или в 19 140 футов, [35]содержит 60 столбов, то, разделив 19 140 на 60, мы находим, что расстояние между двумя соседними столбами составляет 319 футов. Скорость автомобиля, как и длина линии, оказывается не существенной. Однако решение задачи не единственно, если только мы не предположим, что счет столбов, проезжаемых за минуту, начинается и заканчивается в точке, расположенной в промежутке между столбами, и что аналогично определяется и длина телеграфной линии. – М. Г.]

185. Вот эти 5 нечетных «цифр», которые в сумме дают 14:

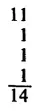
186. На рисунке показан ответ к этой удивительно трудной головоломке.

187. Шахматную доску можно разделить на 18 различных частей, как показано на рисунке.

[Существует много разных способов, какими можно разделить доску на 18 различных частей. В качестве интересного упражнения читатель может попытаться найти доказательство того, что 18 – действительно максимальное число. – М. Г.]

188. Котелок, подобно абажуру, имеет форму усеченного конуса, у которого верхушка отрезана плоскостью, параллельной основанию. Объем такой фигуры можно найти, вычитая из объема конуса объем отрезанной части, или проще по формуле:

πh/3(R 2+ r 2+ Rr).

В этой формуле h означает высоту усеченного конуса, а r и R – соответственно радиусы верхнего и нижнего оснований. В нашем случае высота котла равна 12 дюймам, и один из радиусов вдвое больше другого. Если мы через R обозначим радиус дна, то радиус крышки будет равен 2 R , а объем – 28π/R 2. Поскольку объем равен 25 галлонам, то есть 5775 кубическим дюймам, легко найти диаметр обода, а тем самым и крышки – он чуть превышает 32 дюйма.

189. Каждую неделю добрая леди тратила на благотворительные цели 120 долларов. Первоначально еженедельное «пособие» получали 20 человек.