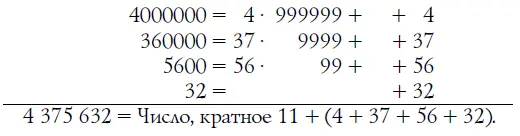Яков Перельман - Живая математика. Математические рассказы и головоломки

Поясним сказанное тремя примерами.

1) Число 154. Разбиваем на грани: 1-54. Складываем:

I + 54 = 55. Так как 55 кратно 11, то и 154 кратно 11:

154: 11 = 14.

2) Число 7843. Разбив на грани (78-43), складываем их: 78+43 = 121. Эта сумма делится на 11, значит, делится и испытуемое число.

3) Число 4 375 632. Разбив на грани, складываем:

4 + 37 + 56 + 32 = 129. Полученное число также разбиваем на грани (1 + 29) и складываем их: 1 + 29 = = 30. Число это не кратно 11, значит, не делится на 11 и число 129, а следовательно, и первоначальное число 4 375 632.

На чем этот способ основан? Поясним это на последнем примере.

Число 4 375 632 = 4 000 000 + 370 000 + 5 600 + 32.

Далее:

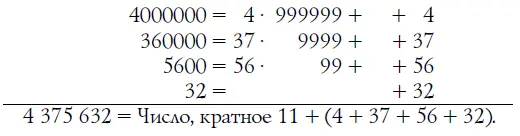
Так как числа 99, 9999 и 999 999 кратны 11, ясно, что делимость нашего числа на 11 зависит от делимости суммы чисел, стоящих в скобках, т. е. суммы граней испытуемого числа.

50. Терпеливый читатель может разыскать девять случаев такого умножения. Вот они:

12x 483 = 5796

42 х 138 = 5796

18 х 297 = 5346

27 х 198 = 5346

39 х 186 = 7254

48 х 159 = 7632

28 х 157 = 4396

4 х 1738 = 6952

4 х 1963 = 7852

51-52. Решения показаны на прилагаемых рисунках 45 и 46. Средние цифры каждого ряда можно переставить и получить таким образом еще ряд решений.

53. Чтобы облегчить себе отыскание требуемого расположения чисел, будем руководствоваться следующими соображениями.

Сумма чисел на концах искомой звезды равна 26; сумма же чисел звезды 78. Значит, сумма чисел внутреннего шестиугольника равна 78-26 = 52.

Рассмотрим затем один из больших треугольников. Сумма чисел каждой его стороны равна 26; сложим числа всех трех сторон - получим 26 х 3 = 78, причем каждое из чисел, стоящих на углах, входит дважды. А так как сумма чисел трех внутренних пар (т. е. внутреннего шестиугольника) должна, как мы знаем, равняться 52, то удвоенная сумма чисел на вершинах каждого треугольника равна 78-52 = 26; однократная же сумма = 13.

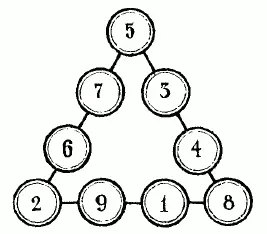
Рис. 45

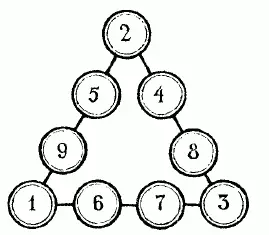
Рис. 46

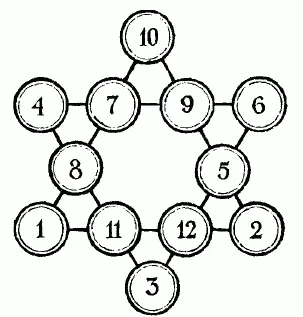
Рис. 47

Поле поисков теперь заметно сузилось. Мы знаем, например, что ни 12, ни 11 не могут занимать вершины звезды (почему?). Значит, испытания можно начинать с

10, причем сразу определяется, какие два числа должны занимать остальные вершины треугольника: 1 и 2. Подвигаясь таким путем далее, мы, наконец, разыщем требуемое расположение. Оно показано на рис. 47.

Революционер-подпольщик вынужден вести свои записи и переписку с товарищами таким образом, чтобы никто из посторонних не мог понять написанного. Для этого пользуются особым способом письма, называемым «тайнописью» (или «криптографией»). Придуманы разные системы тайнописи; к их услугам прибегают не одни подпольщики, но также дипломаты и военные для сохранения государственных тайн. Здесь мы хотим рассказать об одном из таких способов ведения секретной переписки, а именно: о так называемом способе «решетки». Он принадлежит к числу сравнительно простых и тесно связан с арифметикой.

Желающие вести тайную переписку по этому способу запасаются каждый «решеткой», т. е. бумажным квадратиком с прорезанными в нем окошечками. Образчик решетки вы видите на рис. 48. Окошечки размещены не произвольно, а в определенном порядке, который станет ясен вам из дальнейшего.

Рис. 48. Решетка для секретной переписки

Пусть требуется послать товарищу такую записку: «Собрание делегатов района отмените.

Полиция кем-то предупреждена. Антон».

Наложив решетку на листок бумаги, подпольщик пишет сообщение букву за буквой в окошечках решетки. Так как окошек 16, то сначала помещается только часть записки:

Собрание делегато…

Сняв решетку, мы увидим запись, представленную на рис. 49.

Здесь, разумеется, ничего засекреченного пока нет: каждый легко поймет, в чем дело. Но это только начало; записка в таком виде не останется. Подпольщик поворачивает решетку «по часовой стрелке» на четверть оборота, т. е. располагает ее на том же листке так, что цифра 2, бывшая раньше сбоку, теперь оказывается вверху. При новом положении решетки все раньше написанные буквы заслонены, а в окошечках появляется чистая бумага. В них пишут следующие 16 букв секретного сообщения.