Яков Перельман - Живая математика. Математические рассказы и головоломки

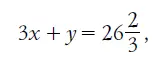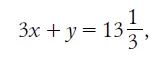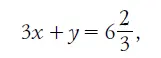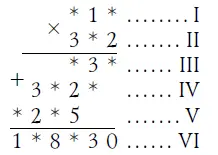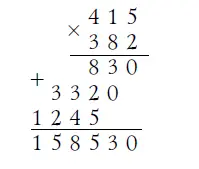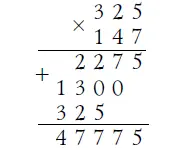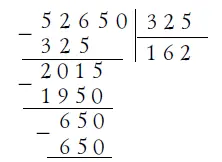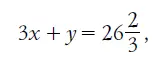
Но Зх, тройное число полтинников, есть, конечно, число целое. Число двугривенных, у, также целое. Сумма же двух целых чисел не может оказаться числом дробным (26 2/ 3). Наше предположение о разрешимости этой задачи приводит, как видите, к нелепости. Значит, задача неразрешима.

Подобным же образом читатель убедится в неразрешимости двух других, «удешевленных» задач: с уплатою 3 и 2 рублей. Первая приводит к уравнению:

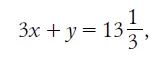
Вторая - к уравнению:

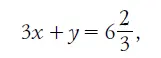
То и другое в целых числах неразрешимо.

Как видите, ни счетчик, ни я нисколько не рисковали, предлагая крупные суммы за решение этих задач: выдать премий никогда не придется.

Другое дело было бы, если бы требовалось уплатить двадцатью монетами названного достоинства не 5, не 3 и не 2 руб., а, например, 4 руб.: тогда задача легко решалась бы и даже семью различными способами [6] Вот одно из возможных решений: 6 полтинников, 2 двугривенных (20-копеечная монета. – Прим. ред.) и 12 пятаков. .

43. 888 + 88 + 8 + 8 + 8 = 1000.

44. Вот два решения:

22 + 2 = 24; З 3 - 3 = 24.

45. Приводим три решения:

6 х 6 - 6 = 30; З 3+ 3 = 30; 33 - 3 = 30.

46. Недостающие цифры восстанавливаются постепенно, если применить следующий ход рассуждений.

Для удобства пронумеруем строки:

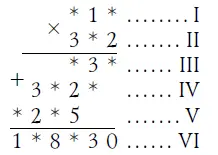
Легко сообразить, что последняя звездочка в III строке цифр есть 0: это ясно из того, что 0 стоит в конце VI строки.

Теперь определяется значение последней звездочки I строки: это цифра, которая от умножения на 2 дает число, оканчивающееся нулем, а от умножения на 3 - число, оканчивающееся пятью (V ряд). Цифра такая только одна - 5.

Нетрудно догадаться, что скрывается под звездочкой II строки: 8, потому что только при умножении на 8 цифра 5 дает результат, оканчивающийся 20 (IV строка).

Наконец, становится ясным значение первой звездочки строки I: это цифра 4, потому что только 4, умноженное на 8, дает результат, начинающийся на 3 (строка IV). Узнать остальные неизвестные цифры теперь не составляет никакой трудности: достаточно перемножить числа первых двух строк, уже вполне определившиеся.

В конечном итоге получаем такой пример умножения:

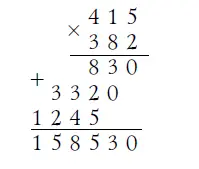
47- Подобным сейчас примененному ходом рассуждений раскрываем значение звездочек и в этом случае. Получаем:

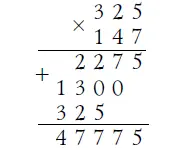
48. Вот искомый случай деления:

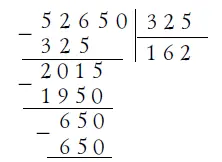
49. Чтобы решить эту задачу, надо знать признак делимости на 11. Число делится на 11, если разность между суммою цифр, стоящих на четных местах, и суммою цифр, стоящих на нечетных местах, делится на 11 или равна нулю.

Испытаем, для примера, число 23 658 904.

Сумма цифр, стоящих на четных местах:

3 + 5 + 9 + 4 = 21,

сумма цифр, стоящих на нечетных местах:

2 + 6 + 8 + 0 = 16.

Разность их (надо вычитать из большего меньшее) равна:

21 - 16 = 5.

Эта разность (5) не делится на 11, значит, и взятое число не делится без остатка на 11.

Испытаем другое число - 7 344 535:

3 + 4 + 3 = 10,

7 + 4 + 5 + 5 = 21,

21 - 10 = И.

Так как 11 делится на 11, то и испытуемое число кратно 11.

Теперь легко сообразить, в каком порядке надо писать девять цифр, чтобы получилось число, кратное 11 и удовлетворяющее требованиям задачи.

Вот пример:

352 049 786.

Испытаем:

3 + 2 + 4 + 7 + 6 = 22,

5 + 0 + 9 + 8 = 22.

Разность 22-22 = 0; значит, написанное нами число кратно 11.

Наибольшее из всех таких чисел есть:

987 652 413.

Наименьшее:

102 347 586.

Пользуюсь случаем познакомить читателей с другим признаком делимости на 11, хотя и не пригодным для решения нашей задачи, зато весьма удобным для практических надобностей. Он состоит в том, что испытуемое число разбивают справа налево на грани по две цифры в каждой и грани эти складывают как двузначные числа. Если полученная сумма делится на 11, то и испытуемое число кратно 11.