Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

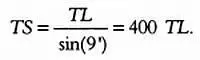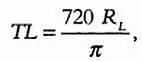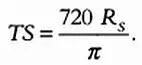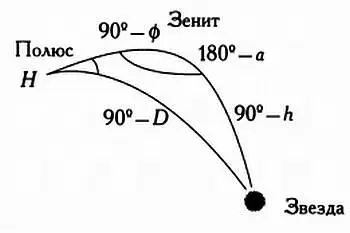
Треугольник полюс — зенит — звезда.

Аристарх Самосский(310 год до и. э. — 230 год до н. э.) определил отношения между расстояниями и радиусами небесных тел в системе «Земля — Луна — Солнце». Он вычислил отношение между радиусом Солнца и радиусом Луны, между расстоянием от Земли до Солнца и расстоянием от Земли до Луны, а также определил отношение радиуса Земли ко всем этим расстояниям. К сожалению, исследователь не смог рассчитать значение радиуса нашей планеты и вычислить абсолютные значения всех остальных радиусов и расстояний. Радиус Земли определил Эратосфен несколько лет спустя. Применив современную нотацию (и современные значения), мы покажем, как действовал Аристарх Самосский, и предложим читателю повторить его эксперимент. Вы убедитесь, что, проведя необходимые наблюдения, нетрудно получить те же результаты, что и древний мыслитель.

Отношение расстояний между Землей и Луной и Землей и Солнцем Аристарх Самосский определил, что угол, под которым с Земли виден отрезок, соединяющий Солнце и Луну, когда Луна находится в первой четверти, равен 87°.

Сегодня мы знаем, что он допустил ошибку — возможно, потому, что определить точный момент, когда Луна находится в первой четверти, очень сложно. Реальное значение этого угла равно 89°51’, в остальном же метод Аристарха Самосского полностью корректен. Обозначим через TS расстояние от Земли до Солнца, через TL — расстояние от Земли до Луны. Так как sin (9’) = TL / TS , имеем:

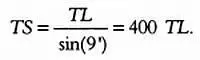
Аристарх Самосский вычислил, что TS = 19 TL .

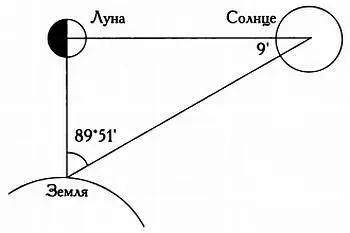
Расположение Луны в первой четверти относительно Земли и Солнца.

Отношение между радиусом Луны и Солнца

Отношение между радиусом Луны и Солнца должно рассчитываться по формуле, похожей на указанную выше, так как при наблюдении с Земли диаметры Луны и Солнца равны 0,5°. Следовательно, выполняется соотношение:

R s = 400 R l .

Отношение между расстоянием от Земли до Луны и радиусом Луны или между расстоянием от Земли до Солнца и радиусом Солнца

Так как диаметр Луны при наблюдении с Земли равен 0,5°, отложив его 720 раз, можно полностью покрыть орбиту Луны (предполагается, что она имеет форму окружности). Длина ее орбиты в 2 π раз больше расстояния от Земли до Луны, то есть 2 R L ∙ 720 = 2 πTL . Выразив из этой формулы TL , имеем:

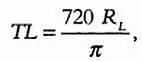
Проведя аналогичные рассуждения и предположив, что Земля вращается вокруг Солнца по окружности радиуса TS ,

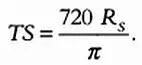
Отношение между расстояниями до Земли и радиусами Луны, Солнца и Земли

Во время лунного затмения Аристарх Самосский заметил, что Луна находится в конусообразной тени Земли в два раза дольше, чем необходимо, чтобы поверхность Луны была полностью покрыта тенью. Он сделал вывод: диаметр конусообразной тени Земли в два раза больше диаметра Луны, таким образом, отношение между этими диаметрами (а следовательно, и радиусами) равно 2:1. Сегодня известно, что отношение радиуса Земли к радиусу Луны равно 2,6:1. Во время лунного затмения с помощью хронометра можно определить отношения интервала между первым и последним соприкосновением границы Луны с конусообразной тенью Земли (этот интервал укажет диаметр конусообразной тени Земли) и интервала, в течение которого поверхность Луны окажется полностью покрыта тенью. Проведя расчеты, нетрудно получить значение, близкое к 2,6:1.

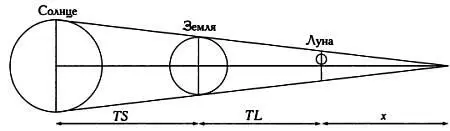
Конусообразная тень Земли и относительное расположение Земли, Луны и Солнца.

Используя обозначения, указанные на иллюстрации, установим следующие соотношения ( х — вспомогательная переменная, которая используется для упрощения расчетов):