Карлос Мадрид - Мир математики. т.32. Бабочка и ураган. Теория хаоса и глобальное потепление

Каким же было удивление ученого, когда он, отдыхая на пляжах Рио-де-Жанейро, получил письмо с контрпримером к своей гипотезе. Норман Левинсон, коллега Смэйла из Массачусетского технологического института (MIT), описал динамическую систему, порождавшую нелинейный осциллятор Ван дер Поля, изученный Картрайт и Литлвудом. Эта система имела бесконечное множество периодических орбит и, что еще хуже, в долгосрочном периоде демонстрировала в высшей степени странное поведение: в теории была возможна ситуация, при которой система в будущем не будет оставаться неподвижной и не будет совершать определенные движения снова и снова, а продолжит двигаться совершенно беспорядочным образом. Рассмотрев аналитические работы Левинсона с геометрической точки зрения, Смэйл в 1959 году описал соленоид Смэйла (названный так за внешнее сходство с соленоидом — электромагнитом, состоящим из металлического сердечника, на который намотана проволока), а затем, уже в 1960-е — подкову Смэйла, обладающую крайне сложной динамикой, схожей с той, что демонстрирует система, описанная Левинсоном. Это были два в высшей степени странных аттрактора.

Соленоид Смэйла, представляющий собой тор, трижды обмотанный вокруг другого тора в четырехмерном пространстве.

Описание соленоида Смэйла, и в особенности подковы Смэйла, стало важным шагом на пути к пониманию связи между существованием гомоклинической орбиты и непериодическим и неустойчивым поведением, которое позднее стало называться детерминированным хаосом. С мэйл доказал, что существование гомоклинических точек подразумевает существование подковы — фигуры, служащей воплощением топологических операций растяжения и складывания, которые, как мы объясним в третьей главе, порождают хаос.

Возьмем на себя смелость рассмотреть хаос подробнее. До сих пор мы пытались приблизиться к хаосу с помощью интуитивно понятных примеров, однако понять, что же происходит на самом деле, совсем не просто. В научно-популярных книгах и даже в учебниках объяснения начинаются с числовых примеров, и только потом автор приводит примеры из геометрии и топологии.

Мы же решили действовать противоположным образом: во-первых, именно так исторически изучался хаос, во-вторых, так читатель сможет лучше понять, как и математики постепенно понимали, что такое хаос, — сначала с качественной, а затем с количественной точки зрения. У вас кружится голова от непонятных слов? Не беспокойтесь, математики прошлого чувствовали себя точно так же.

И соленоид, и подкова Смэйла — это примеры отображений, геометрических преобразований, в которых проявляется хаос. Преобразование, порождающее подкову Смэйла (обозначим его через f ), очень простое. Чтобы выполнить его, рассмотрим квадрат или любую другую фигуру похожей формы. Сначала расположим квадрат на плоскости, растянем его, затем сложим пополам в форме подковы и уложим в границы, определенные краями исходной фигуры. Если мы будем повторять преобразование f снова и снова бесконечное число раз, то получим сложную и запутанную многослойную структуру, и возникнет хаос. На первой итерации исходный квадрат превратится в подкову в форме буквы U , как показано на следующем рисунке. На второй итерации подкова превратится в другую подкову, состоящую из трех кривых в форме буквы U . На третьей итерации мы получим уже семь кривых той же формы, и так далее. В пределе имеем бесконечно запутанную кривую, очень похожую на гомоклиническую сеть, которая приводила в ужас Пуанкаре. И действительно, в растяжении и складывании заключен геометрический смысл хаоса.

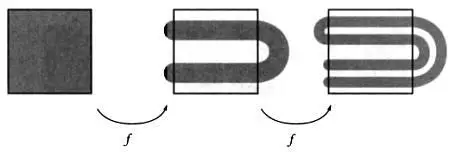
Последовательные итерации при построении подковы Смэйла. Они заключаются в растяжении и складывании кривой в форме буквы U в границах исходной фигуры.

Последовательно выполняемые операции растяжения и складывания, характерные для подковы Смэйла, — верный признак хаоса. Следовательно, эти же операции вы встретите во многих хаотических отображениях. В качестве примера можно привести «отображение пекаря», названное так за сходство с операциями, выполняемыми при замешивании теста, или «отображение кота Арнольда», определенное В. И. Арнольдом (о нем мы расскажем позже), которое заключается в последовательном растяжении и складывании изображения головы кота. Но мы не будем растягивать и складывать голову кота, вместо этого используем более привлекательное изображение — фотографию модели Лины Седерберг, мисс Ноябрь журнала «Плейбой» 1972 года. С 1970-х годов фрагмент ее фотографии используется в качестве тестового изображения в алгоритмах сжатия изображений и, по сути, является стандартом в науке и технике. (И кто-то еще осмеливается заявлять, что математики — скучные люди!) Между прочим, номер «Плейбоя» с этой фотографией стал самым продаваемым за всю историю журнала.