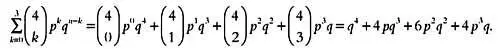Неравенству с одной переменной х— 7 > 13 удовлетворяют все числа, которые при уменьшении на 7 равняются 13 или более. Неравенства решаются по схожему алгоритму. Пример:
х— 7 >= 13; х— 7 + 7 >= 13 + 7; х>= 20.
Решением этого неравенства является множество всех чисел, больших или равных 20.
Иногда уравнения и неравенства ведут себя по-разному, как, например, в следующем случае.
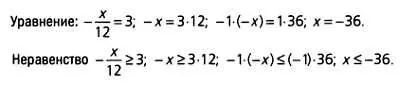
Здесь для решения неравенства нужно сменить его знак на противоположный.
Это можно показать так: 7 < 13, однако, напротив, — 7 > — 13.
* * *
Сумма первых восьми нечетных чисел записывается следующим образом:
Σ n j=0 (1 + 2j) = (1 + 2∙0) + (1 + 2∙1) + (1 + 2∙2) + (1 + 2∙3) + (1 + 2∙4) + (1 + 2∙5) + (1 + 2∙6) + (1 + 2∙7) + (1+ 2∙8) = 1 + 3 + 5 + 7 + 9 + 11+ 13 +15 + 17.
Сумма Σ 5 j=2 2 jравняется 2 2+ 2 3+ 2 4+ 2 5= 4 + 8 +16 + 32.
Сумма Σ 3 l=1 (l+1)∙3 l= 2∙З 1+ 3∙З 2+ 4∙3 3= 6 + 27 + 108.
* * *
ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ ПЕРЕМЕННЫЕ
Во многих областях современной математики переменная определяется как дискретное множество (это означает, что она может принимать только определенные значения, и между двумя соседними значениями не может находиться никакого другого). На языке математики это записывается так: { х 1, х 2, …, х n}. Между значениями х 1и х 2нет никакого другого значения переменной х.
Существуют и другие переменные, используемые намного чаще, которые определены на непрерывных множествах (это означает, что такие переменные могут принимать целые, дробные и иррациональные значения). Примером такой переменной является {0 <= t <= }. Очень часто для решения различных задач, связанных с функциями, определенными на непрерывных множествах, требуется выполнить операцию интегрирования 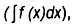 , как, например, в случае с функцией вероятности или нормальным распределением вероятности. Когда речь идет о дискретных переменных, операцией, аналогичной интегрированию, является сложение.
, как, например, в случае с функцией вероятности или нормальным распределением вероятности. Когда речь идет о дискретных переменных, операцией, аналогичной интегрированию, является сложение.
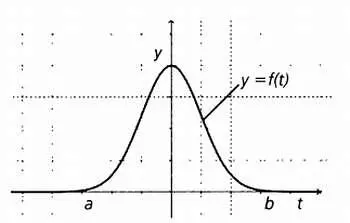
Функция f(t)непрерывной переменной t, определенная на множестве { a<= t<= b}.
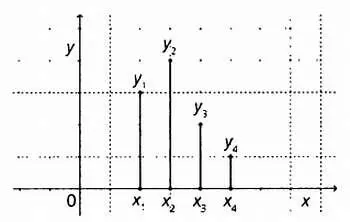
Функция у(х)дискретной переменной х, определенная на множестве { х 1, х 2, х 3, x 4}.
Множество из четырех элементов можно обозначить буквами и цифрами, которые будут выступать в качестве индексов: х 1, х 2, х 3, x 4.Если мы хотим работать с множеством из nэлементов ( nможет изменяться в зависимости от задачи), они будут обозначаться { х 1, х 2…. х n-1, x n}. Так, х n - 1обозначает элемент, идущий перед х n, последним элементом множества. Произвольный элемент ряда (занимающий в нем i-е место) обозначается х i. Таким образом, например, цены четырех товаров можно обозначить p 1, р 2, р 3и р 4, а запрошенные объемы каждого товара — q 1, q 2, q 3и q 4.
* * *
Определенная сумма применяется при записи математических рядов, например биномиального ряда. Биномиальное распределение вероятности используется при анализе результатов опросов, когда на вопрос возможны лишь два ответа (например, «да» и «нет»). Вероятность их появления равняется ри q. А поскольку сумма их вероятностей равна р+ q= 1, следовательно, q = 1 — р.
Чтобы узнать вероятность того, что будет получено три или менее ответа «да», нужно вычислить вероятности следующих событий: ни одного ответа «да», один ответ «да», два ответа «да» или три ответа «да», то есть Р (0 < k < 3) = Р (0) + Р (1) + Р (2) + Р (3). Эту же формулу можно записать так:
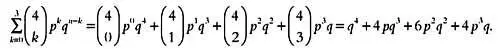
Функция, позволяющая вычислить вероятность того, что на п вопросов будет дано от 0 до kответов «да», равна сумме вероятностей, последним слагаемым в которой будет Р(k). Эта же формула записывается в следующем виде:
Читать дальше

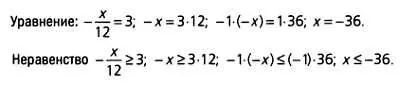
 , как, например, в случае с функцией вероятности или нормальным распределением вероятности. Когда речь идет о дискретных переменных, операцией, аналогичной интегрированию, является сложение.
, как, например, в случае с функцией вероятности или нормальным распределением вероятности. Когда речь идет о дискретных переменных, операцией, аналогичной интегрированию, является сложение.