Луис Арталь - Том 19. Ипотека и уравнения. Математика в экономике

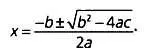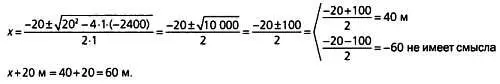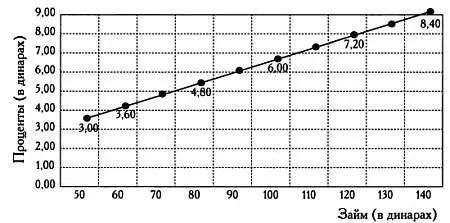
Правило пропорции.

Похожи на них задачи с обратной пропорциональностью. Два каменщика строят стену за 12 дней. Сколько дней понадобится на постройку стены пяти каменщикам?

2 человека ___ 12 дней

5 человек ____ хдней.

Задача решается следующим образом:

2/5 = х/12

2∙12 = 5 х

5 х/5 = 2∙12/5

х= 2∙12/5 = 4,80 дня = 4 дня 19 часов 12 минут.

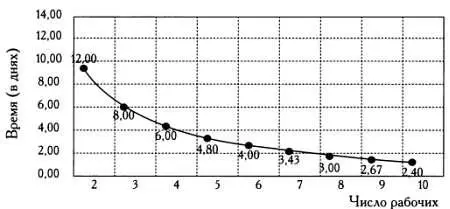
Второй вариант использования правила пропорции.

Наконец, правило пропорции применимо и для решения более сложных задач: если 40 маляров, работая по 8 часов в день, красят 320 метров забора за 10 дней, то за сколько дней 55 маляров покрасят 440 метров такого же забора, если будут работать по 6 часов в день?

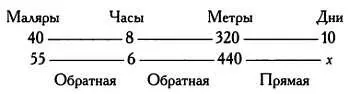
Задача решается следующим образом:

10/ х= 55/40∙6/8∙320/440

х= 10∙440/320∙8/6∙40/55 = 13,3 дня = 13 дней 8 часов.

Греческая буква Σ(заглавная сигма) очень часто используется в математических формулах экономической теории и обозначает сумму слагаемых. Например, для обозначения суммы x 1 + х 2+ х 3 + х 4 можно использовать выражение Σ 4 i=1x i

Знак Σперед х i означает, что нужно сложить все значения х. Числа, указанные под буквой Σи над ней, обозначают границы суммы, то есть наибольшее и наименьшее значение индекса, которое используется при сложении.

Сумма Σ 6 k=3x kозначает х 3+ х 4+ х 5+ х 6,

Cумма Σ n j=mx jозначает х m+ х m+1 … + х n-1+ х n.

Индексы могут принимать только целые значения, а нижний индекс может быть обозначен любой буквой.

Так, Σ m i=1x i = Σ m j=1x j = Σ m k=1x k

Член, следующий за буквой Σ, называется слагаемым. В выражении Σ m k=1x kслагаемыми являются х k.

* * *

УРАВНЕНИЯ И НЕРАВЕНСТВА

Уравнение — это математическое равенство с одной или несколькими неизвестными величинами.

Уравнение обращается в верное равенство лишь при определенных значениях этих неизвестных. Неизвестная в уравнениях может быть возведена в квадрат или в куб.

Например, х + 12 = 25 — Зх — уравнение первой степени, 12 + х 2— 6х = 3 — уравнение второй степени, 9 — Зх 2— 6х 3= -12 — уравнение третьей степени.

В XIII веке Леонардо Пизанский решал задачи, подобные следующей: у ювелира есть золото 975-й пробы и золото 750-й пробы, и он хочет получить слиток золота 900-й пробы весом в два килограмма.

Сколько золота каждой пробы потребуется для этого? Эта задача решается так:

хкг вес золота 975-й пробы

(2 — х) кг вес золота 750-й пробы

х∙0,975 + (2 — х)∙0,750 = 2∙0,900

х∙0,975 + 2 0,750 — 0,750∙ х= 1,800

х∙0,975 — 0,750 х= 1,800 — 2∙0,750

х∙0,225 = 1,800 — 1,500

х∙0,225 = 0,300

х= 0,300/0,225 = 4/3 = 1 1/3 кг золота 975-й пробы

(2 — х) = 2 – 1 1/3 = 2/3 кг золота 750-й пробы.

Фибоначчи также сформулировал и решил задачи, описываемые уравнениями второй степени, подобные следующей: площадь прямоугольного поля равна 2400 м 2Известно, что его длина на 20 м больше ширины. Вычислите размеры поля. Таким образом, произведение ширины ( х) на длину ( х+ 20) равно 2400 м 2. Стандартное уравнение второй степени выглядит так: ах 2+ Ьх+ с = 0. Значение неизвестной х можно вычислить по формуле:

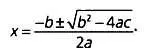
В этом случае:

х∙ (х+ 20) = 2400; х 2+ 20х= 2400; х2+ 20х— 2400 = 0.

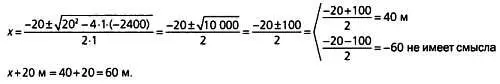
Таким образом, поле имеет размеры 40 х 60 м.

Неравенства похожи на уравнения, однако вместо знака равенства (-) содержат один из четырех возможных знаков неравенства:

<= «меньше либо равно»

< «меньше» (строго)

>= «больше либо равно»

> «больше» (строго).