Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

А “чистая” мажорная терция возникнет с помощью соотношения ми и до как 5:4.

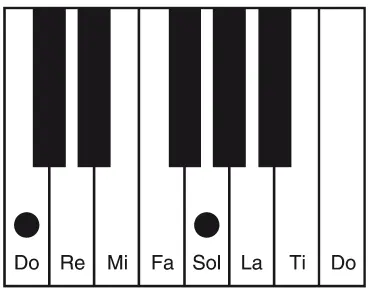
Наконец, кварты над до мы добьемся с помощью струны, длина которой будет относиться к исходной как 4:3.

Остается заполнить три звука в гамме. Интервал от до до си называется септимой (если считать от до, си – это седьмая ступень гаммы). Однако эта нота также является большой терцией от соль, поэтому рассчитать ее параметры нетрудно: можно использовать струну, длина которой относится к соль в пропорции 5:4. Точно так же ля легко добиться, рассчитав большую терцию от фа.

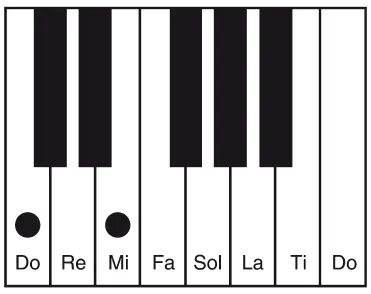
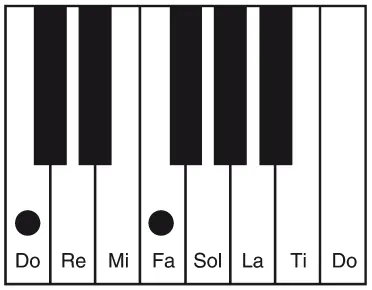
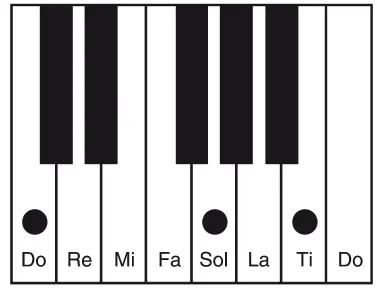
И, наконец, ре можно рассчитать, отступив от соль на кварту вниз.

Итак, звукоряд чистого строя готов – однако в нем обнаруживается немало проблем. Некоторые звуки мы рассчитали, отталкиваясь от пропорций чистой квинты, другие – от большой терции. В итоге наши интервалы оказались разного размера, в нашей гамме нет единого, унифицированного “шага” между нотами. Получается, что расстояние от до до ре не равно расстоянию от ре до ми – и то же самое касается соотношения расстояний между фа и соль, а также соль и ля.

Сугубо музыкальные последствия этого могут быть достаточно тяжелыми. Некоторые интервалы звучат восхитительно чисто: например, созвучия, образованные большой терцией или чистой квинтой от до, фа или соль.

Но при попытке образовать такое же созвучие от ре нас ждет провал. Мы удостоверились, что наше ля образует идеальную большую терцию от фа, но из-за этого соотношение между ре и ля не дает чистой квинты – расстояние между этими нотами оказывается короче, чем искомые 3:2. Поэтому зажав одновременно ноты ре, фа и ля и ожидая их гармоничного сочетания, мы получим на выходе чудовищный, немузыкальный скрежет.

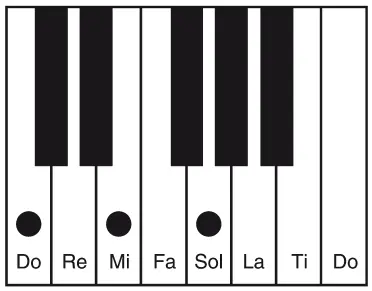
Однако если попытаться подстроить этот интервал – например, слегка изменить высоту ноты ре, так что она образует чистую квинту с ля, – это автоматически испортит ее созвучие с соль. Это противоречие кажется неразрешимым.

Некоторые музыканты, например друг Леонардо да Винчи, композитор, учитель и священник Франкино Гафури, громко протестовали против подхода Рамоса и продолжали отстаивать идеалы пифагорейского строя. Однако в то же время, пока спорщики с обеих сторон придумывали все новые доказательства истинности их воззрений, появился и совершенно новый метод, о котором упоминают в своих трудах и Гафури, и Рамос. Органисты той эпохи, писал Гафури в своей “Музыкальной практике”, законченной в 1483 году, укорачивали трубы своих инструментов, таким образом снижая расстояние, требуемое для квинты, “на некую маленькую, незаметную, неопределенную величину”. Эта практика получила название темперации , или партиципаты.

На первый взгляд, описание кажется очень расплывчатым – и с весьма сомнительным смыслом. Но в действительности “партиципата” Гафури, как и архимедова “Эврика!”, возвещает открытие невероятной важности. Факт в том, что описанные органисты, в отличие от Рамоса или Гафури, вовсе не были озабочены поиском “идеального” строя. Они преследовали совершенно иные, утилитарные цели. В их варианте разрешения великого клавишного парадокса оказался изменен фундаментальный принцип: на место фанатичного стремления к “чистоте” пришла стратегия допустимых потерь. Чтобы музыкальный инструмент был пригоден для использования, нужно было принести в жертву священные квинты – и они пошли на это.

Многим этот шаг казался не менее опасным, чем, например, изъятие центральной несущей балки из строительной конструкции – соверши что-нибудь подобное, и все здание обрушится, погребя под обломками тех, кто находится внутри. Тем не менее у описанной музыкальной практики было и весьма элегантное обоснование. Как мы уже видели, в инструменте, настроенном традиционным образом, через последовательность чистых квинт, терции оказываются невыносимыми, как капли уксуса, попавшие в уши. Подобной, мягко говоря, неудовлетворительной терции можно достичь, сымитировав процедуру, использованную Пифагором для обнаружения квинт на монохорде: установить ноту до, отсчитать от нее квинту – соль, затем квинту от соль – ре, и так далее; в конечном счете мы найдем до, соль, ре, ля и ми, а затем от каждого из этих тонов протянем октавы по всей клавиатуре.