Стюарт Исакофф - Музыкальный строй. Как музыка превратилась в поле битвы величайших умов западной цивилизации

Возьмем для начала струну средней длины и присвоим ей ноту, которую мы называем “до” (сейчас есть стандартная длина струны для до, но мы находимся в Средневековье и собираем средневековый инструмент). Чтобы затем установить верные длины для прочих нот на клавиатуре, вспомним о пропорциях, найденных Пифагором. Для ноты соль, которая находится выше на расстоянии чистой квинты, мы используем более короткую струну, которая будет относиться к до как 3:2. Иными словами, наша струна-соль (при условии, опять-таки, что материал и сила натяжения всех струн одинаковы) будет на треть короче струны-до.

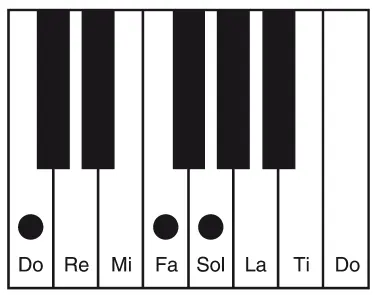
Струну для ноты фа мы подберем, использовав формулу чистой кварты от до: они будут соотноситься друг с другом как 4:3.

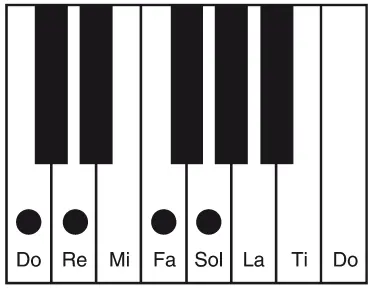
Затем найдем нужную струну для ноты ре, отступив от уже имеющейся у нас ноты соль чистую кварту вниз. И вновь пропорция будет 4:3, более низкая нота получит в свое распоряжение более длинную струну.

Пока все идет как по маслу. Вскоре, однако, возникают трудности – например, с определением длины струны для ноты ля. Ведь вариантов уже больше одного. К примеру, ля находится на расстоянии чистой квинты от ре, и их соответственные длины должны образовать пропорцию 3:2. Однако ля также представляет собой большую терцию от фа, так что этот тон можно сформировать, разместив эти две струны в соотношении 5:4. Проблема в том, что при выборе этих вариантов звуки получатся разными. И какой же из них является настоящим ля?

Это – самый важный вопрос. Интервал между фа и ля, созданный в пифагорейской настройке – то есть через последовательность чистых квинт (3:2), – будет немного шире той “чистой” терции (5:4), которая так приятна на слух, и в результате его звучание куда менее красиво – оно оказывается резковатым, немного кислым. С другой стороны, то ля, которое так прекрасно сочетается в большой терции с нижним фа, образует недопустимый диссонанс в созвучии с нижним ре, то есть со своей квинтой.

Разница между этими двумя вариантами ля называется коммой (в данном случае – Дидимовой, по имени древнего грека, впервые ее описавшего, или синтонической коммой). В грамматике комма, она же запятая, означает паузу – короткую остановку в предложении, предназначенную, например, для того, чтобы набрать воздух в легкие. В музыке этот термин тоже описывает небольшой провал: несовпадение двух тонов, которые близки друг другу настолько, чтобы называться одинаково, однако при этом высчитаны с помощью разных пропорций. И так же, как поставленная не к месту запятая способна убить целую фразу, так и шальная музыкальная комма со скрежетом остановит лирическую тему. Более того, в музыке даже бесконечно малая “дыра” такого рода становится звуковым аналогом гигантской пропасти.

Терции – не единственный “проблемный” интервал на клавиатуре. Как мы убедились, еще Пифагор несколько тысяч лет назад обнаружил несовершенство в ряду чистых квинт: чтобы двенадцать звуков, сгенерированных в пропорции 3:2 по отношению друг к другу, прошли полный круг от “до” до “до” этот самый круг должен быть слегка “подрихтован”. Другими словами, одно из звеньев в этой цепочке необходимо чуть-чуть укоротить (на расстояние, которое называется пифагорейской коммой) – и тогда верхняя нота последовательности образует идеальную октаву с ее нижней тезкой. Но в действительности процесс искусственной подгонки квинт описанным выше способом обречет то самое укороченное звено на весьма печальную судьбу: звуки, из которых оно будет состоять, в сочетании друг с другом дадут корявую, воющую “волчью” ноту, которой необходимо будет избегать.

Таким образом, настройка всех соотношений нот в клавишном инструменте с чистыми квинтами в качестве единицы измерения не работает. Однако то же самое можно сказать и про большие терции: при попытке установить длины струн по их формуле (5:4) мы придем к столь же печальному результату. Теоретически три большие терции дают в совокупности октаву – но на практике это оказывается не так. Сравните три чистые большие терции, каждая в строгом соотношении 5:4, с чистой октавой, и их конечные тона не совпадут друг с другом. Наши старые знакомые плотники никогда не смогут сконструировать годящиеся к использованию книжные полки, если один возьмет за свою меру терции, а другой – октавы.