Банеш Хофман - Альберт Эйнштейн. ТВОРЕЦ И БУНТАРЬ.

Что же касается Резерфорда, то он, как в свое время Максвелл, стал директором знаменитой Кавендишской лаборатории в Кембриджском университете. Теоретик Бор и экспериментатор Резерфорд поддерживали тесную связь, и под их вдохновенным руководством атомная физика шла вперед семимильными шагами.　

Тем не менее не далее как в 1922 г. теория Бора столкнулась с серьезными трудностями. Все — и в первую очередь сам Бор — понимали, что эта теория была лишь продуктом переходного периода в развитии физики. Бор проявил большую изобретательность и расширил ее рамки, введя «принцип соответствия» (запомним этот термин). Это придало ей новую поддержку со стороны неквантовой, классической физики. Однако принцип соответствия имел все признаки временной меры. Становилось ясно, что теория Бора почти исчерпала свои ресурсы, и, поскольку не было, казалось, даже намека на другую теорию, способную занять ее место, теоретики атомной физики пребывали в состоянии глубокой безысходности.　

Но вскоре словно внезапный взрыв смел все препятствия к дальнейшему прогрессу. Как выяснилось, необходимые намеки имелись-таки в достаточном количестве, и всего за несколько лет напряженных и беспорядочных поисков вся картина преобразилась. Не пытайтесь во что бы то ни стало разобраться в том, что последовало далее. В общих чертах это рассказ о нагромождении событий и самых невероятных интерпретаций, которые способны были поставить в тупик даже величайшие умы. И если это и впрямь покажется лишенным всякой упорядоченности, то по крайней мере поможет создать какое-то впечатление о тех судорожных усилиях, которые предпринимали ученые, пытаясь найти выход из создавшегося положения.　

Когда французский физик Морис де Бройль вернулся со знаменитого Сольвеевского конгресса 1911 г., его рассказы о возникших на этом конгрессе дискуссиях взволновали его младшего брата, Луи де Бройля, пожалуй, еще сильнее, чем рассказ Резерфорда об этом конгрессе — молодого Бора. И загадка квантов, и противоречивые факты, подтверждающие, с одной стороны, корпускулярное, а с другой — волновое строение света, не давали покоя Луи де Бройлю, и он между 1922 и 1924 гг. разработал фантастическую на первый взгляд теорию. Свет, считал де Бройль, состоит из частиц, сопровождаемых и направляемых волнами. И — что еще важнее, — по его мысли, точно так же сопровождаются волнами электроны, причем эти волны распространяются со скоростью, превышающей скорость света. Это вполне может показаться неправдоподобным. Да и в самом деле, предложенная де Бройлем интерпретация разработанного им математического аппарата не выдержала проверки, зато ему удалось наглядно объяснить с помощью волн разрешенные электронные орбиты Бора.　

Редкостной проницательностью обладал человек, который принял идеи де Бройля всерьез. Это был Поль Ланжевен. Он и сообщил о работе де Бройля Эйнштейну.　

Случилось так, что незадолго до этого Эйнштейн и сам имел прекрасный случай проявить свою несравненную физическую интуицию. Не известный ему до тех пор индийский физик Ш. Н. Бозе прислал ему свою рукопись. Однако, прежде чем мы о ней расскажем, попробуем ответить на простой вопрос: если подбросить десятицентовую и двадцатипятицентовую монетки, каковы шансы на то, что выпадут два «орла»? Эта элементарная задачка без труда решается в теории вероятностей. Существуют четыре возможности, и все они в равной степени вероятны. Лишь в одном из этих четырех вариантов выпадают два «орла». Поэтому можно ожидать, что при достаточно долгом подбрасывании монет пара «орлов» будет выпадать в среднем в четверти случаев. Итак, шансы один к четырем, и вероятность составляет 1/ 4.

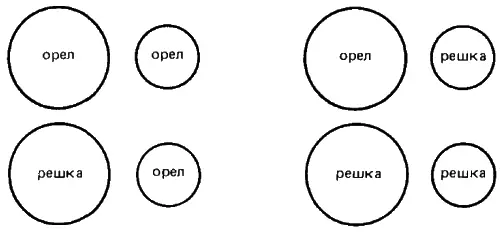
Представим теперь, что мы подбрасываем два новеньких десятицентовика. Очевидно, шансы на выпадение двух «орлов» должны остаться теми же, т. е. один к четырем. Вообще сохраняются в точности те же четыре возможности, однако две из них теперь одинаковы, а именно: когда одна монета упадет «орлом», другая «решкой». Это наводит нас на мысль, что имеются всего три различающихся между собой случая: два «орла», «орел» и «решка», и две «решки». В результате мы можем прийти к ошибочному выводу о том, что шансы на выпадение двух «орлов» составляют не один к четырем, а один к трем. Допустить подобную ошибку действительно нетрудно, но позорна она только для специалистов.