Банеш Хофман - Альберт Эйнштейн. ТВОРЕЦ И БУНТАРЬ.

С отъездом Эйнштейна из Цюриха в Берлин в 1914 г. его совместная работа с Гроссманом практически прекратилась, так и не принеся желаемых результатов. Тем не менее значение этого сотрудничества двух ученых трудно переоценить, ибо Гроссман вооружил Эйнштейна адекватным его целям конкретным математическим аппаратом для продолжения борьбы в Берлине уже в одиночку.

Невозможно рассказать здесь обо всех трудностях, которые пришлось преодолеть Эйнштейну. В течение двух лет он шел по неверному пути, прежде чем разобрался (в числе прочего), что с физической точки зрения нет никаких доводов против равенства всех систем координат и что принцип общей ковариантности в конечном счете не противоречит причинности. После этого дела пошли быстрее, и к 1915 г. Эйнштейну удалось вывести уравнения гравитационного поля, над которыми он так долго бился. Выдвинутая им теория отличалась изумительной простотой и изяществом. Гравитация представлена в ней не силой, а искривлением, внутренне присущим пространству — времени. Небольшие тела — такие, например, как планеты, — движутся вокруг Солнца по орбитам не под действием солнечного притяжения, а потому что в искривленном пространстве — времени вокруг Солнца просто не существует прямых мировых линий. Прямую линию можно определить как кратчайшее расстояние между двумя точками. В искривленном пространстве — времени движение планет было представлено посредством геодезических линий — аналогов кратчайших [25] В силу причудливости пространства — времени с математической точки зрения правильнее было бы сказать здесь не «кратчайшее», а «длиннейшее», но это, с другой стороны, внесло бы в наш рассказ некоторую путаницу. расстояний. Таким образом, движение планет, подобно движению свободных частиц, также подчиняется первому закону Ньютона — закону инерции — в той мере, в какой это возможно в искривленном пространстве — времени. Понять эту мысль нам помогут два рисунка. На одном из них показано на двумерной плоскости нечто вроде трехмерного гравитационного искривления пространства вокруг Солнца, причем кривизна эта для наглядности сильно преувеличена. Из-за этой кривизны планета, находящаяся в точке P и стремящаяся к прямолинейному движению по горизонтали, не сможет его осуществить, а будет двигаться по траектории типа линии PQ . Отсюда становится в какой-то мере понятным, как получилось, что планеты вращаются вокруг Солнца.

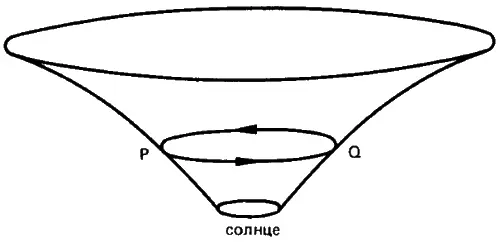
Недостатком этого рисунка является, однако, то, что на нем не показано ни время, ни искривление времени. И хотя, с одной стороны, это вполне корректно с математической точки зрения, с другой стороны — это в корне неправильно. Ведь ведущий фактор, воздействующий на движение планет, — это не искривление пространства, а искривление времени, которое, как оказывается, может быть связано с изменяющейся скоростью света в гравитационном поле. Итак, мы, к собственному удивлению, вернулись к давнишней мысли Эйнштейна о том, что скорость света можно рассматривать в качестве гравитационного потенциала, и это еще одно свидетельство силы научной интуиции Эйнштейна. Кривизну времени нельзя изобразить столь же наглядно, как кривизну пространства. Не будем пытаться сделать это, а просто введем на втором рисунке еще одно измерение — время — и обозначим его как направление снизу вверх. Двойной линией показано положение Солнца в каждый момент времени — иначе говоря, это мировая линия Солнца. Закрученная в виде спирали линия — это мировая линия планеты, т. е. геодезическая линия в искривленном пространстве — времени, связанном с Солнцем. Представим себе, что мы находимся на какой-то платформе, символизирующей «настоящий момент». Поскольку «настоящий момент» движется в будущее, то платформа, на которой мы стоим, будет на рисунке подниматься вверх — напомним, что мы условились изображать время направленным снизу вверх. По мере подъема платформы вверх спираль будет пересекать ее, и каждая из последовательного ряда точек пересечения будет представляться на платформе конкретной точкой околосолнечной орбиты.　

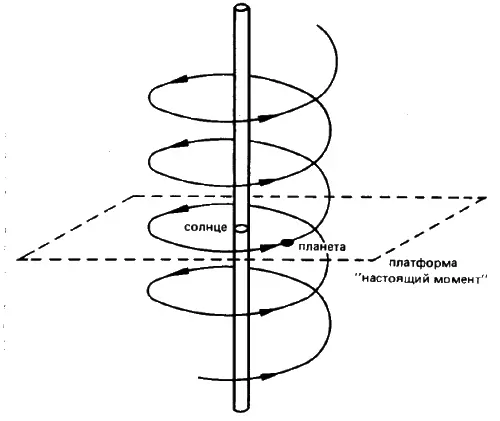
Оба рисунка заведомо далеки от совершенства. В то же время каждый по-своему отражает суть дела. И если нам удастся без особого напряжения сохранить их в памяти, то мы сумеем не так уж плохо представить себе мир, каким его увидел Эйнштейн.