Банеш Хофман - Альберт Эйнштейн. ТВОРЕЦ И БУНТАРЬ.

Гениальные научные идеи не появляются сразу в законченном виде. Интуитивно предчувствуя истину, Эйнштейн еще долго должен был идти к ней. По какому пути предстояло пойти его мысли теперь? Эйнштейн обратился к воздействию гравитации на скорость света. Ведь этот вопрос выходил за рамки специальной теории относительности, согласно которой скорость света постоянна и одинакова для любого наблюдателя. Кроме того, к этому времени физики уже более ста лет привыкли считать, что ньютоновское «действие на расстоянии», т. е. закон гравитации, может быть выражен единственным «уравнением поля», содержащим одну-единственную переменную математическую величину, называемую гравитационным потенциалом. Нельзя ли сделать так, чтобы переменная скорость света играла ту же роль, что и ньютоновский гравитационный потенциал, но уже с релятивистских позиций? Эта конкретная и в то же время обобщающая идея естественным образом привлекала Эйнштейна. Однако попытки ее разработать убедили его в том, что создание приемлемой теории гравитации не может быть осуществлено столь легким способом. Это первое столкновение с трудностями было необходимой разведкой перед главным сражением. Ведь если переменная скорость света на давала адекватного математического представления гравитации, то что же в таком случае могло помочь?

Давайте вернемся к нашим Aclab и Gravlab. Если бы Aclab двигалась без ускорения, то внутри нее свободные частицы двигались бы прямолинейно с постоянной скоростью. Так гласит первый закон Ньютона, а именно закон инерции. Стоит включить ускорение, и те же самые свободные частицы в Aclab, движение которых не изменится, станут как бы падать — точь-в-точь как они падали бы под воздействием силы тяготения в Gravlab.

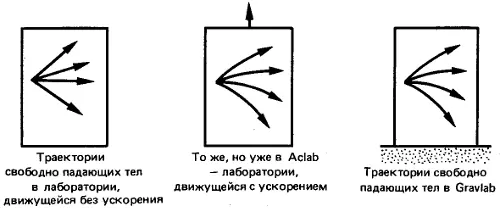
Итак, Эйнштейн разработал «план кампании», который мы и постараемся изложить в упрощенном виде. Во-первых, выразим закон инерции в его релятивистской форме, согласно которой в пространстве — времени мировые линии свободных частиц представляют собой прямые. Затем применим некоторое математическое преобразование для описания ситуации в Aclab. Полученное представление должно автоматически описывать физическую ситуацию в Gravlab; таким образом, можно будет получить какой-то намек на то, как следует рассматривать гравитацию с математической точки зрения.　

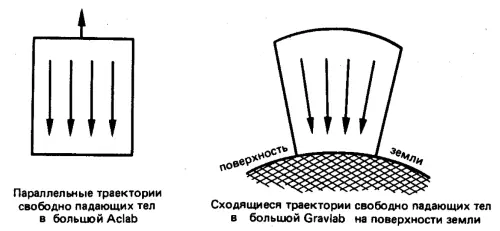
Но почему речь идет только о намеке, а не о законченной теории? Дело в том, что полученные таким путем результаты отражают сугубо локальные свойства гравитации. Если бы АсlаЬ и СгауlаЬ имели большие размеры, они бы уже не были полностью эквивалентны, в чем нетрудно убедиться, взглянув на рисунок, на котором большая космическая АсlаЬ сравнивается с большой СгауlаЬ, расположенной на изогнутой поверхности Земли.

И хотя намек — всего-навсего намек, в запутанной ситуации, как известно, он может представлять большую ценность. В данном же случае этот намек, казалось, приобретал все большее значение, ибо благодаря ему Эйнштейн натолкнулся на целый сонм взаимосвязанных проблем. Искривление времени под воздействием гравитации привело его к мысли, что пространство, теснейшим образом связанное в релятивистской теории со временем, также должно быть искривлено. Более того, ускоренное движение лаборатории вызывает искажение пространственно-временной системы координат — четырехмерного аналога миллиметровой бумаги, — а подобные искажения означают, что эти системы координат утрачивают прямую связь со стандартными часами и масштабами длины. Непосредственные физические измерения стали, таким образом, невозможны, и Эйнштейн испытал крайнюю растерянность. Прошло немало времени, прежде чем он понял, что и здесь содержался намек, притом немаловажный. Эйнштейн вынужден был полностью пересмотреть все, что связано с координатами и измерениями, а это было делом далеко не легким.　

Необычайно важная догадка, которая помогла Эйнштейну найти ключ к этой проблеме и продолжить свои поиски, осенила его не сразу. Попробуем понять его мысль с помощью довольно простой аналогии. Столкнулись два автомобиля. Полиция устанавливает «координаты» — место (пусть это будет угол 20-й стрит и 15-й авеню) и время катастрофы. Теперь изобразим на миллиметровке план района с координатами 20 и 15 и с его помощью легко определим расстояние, которое нужно проехать до места происшествия, например от полицейских участков на 5-й стрит и 8-й авеню. Затем предположим, что катастрофа произошла на углу Кингс Лэйн и Линден Крес- цент, а полицейские участки расположены на Хайлэнд Террас и Болтон Плейс [23] В первом случае говорится о районе Нью-Йорка, где стрит и авеню расположены перпендикулярно друг к другу, образуя как бы прямоугольную сетку. Во втором случае столь строгий порядок отсутствует. — Прим. перев. . С такими координатами мы получим на плане беспорядочную картину города с кривыми и неравномерно расположенными улицами. В таком городе мы без карты не сумеем получить ни малейшего представления о величине искомых расстояний.