Тибо Дамур - Мир по Эйнштейну. От теории относительности до теории струн

В целом мы видим, что квадрат интервала между двумя событиями в зависимости от его знака, по существу, измеряет либо квадрат расстояния, либо квадрат продолжительности времени (умноженный на квадрат скорости света). Мы также видим, что скорость света играет роль фактора перехода от продолжительности к расстоянию. Для простоты удобно использовать единицы, в которых нет необходимости явно вводить этот фактор. Для этого достаточно, например, измерять продолжительности в секундах, а расстояния – в «световых секундах». Напомним, что световая секунда означает расстояние, пройденное светом в течение секунды (так же, как «световой год» определяет расстояние, которое свет преодолевает за год). Световая секунда, таким образом, равна 300 000 км. В этих единицах скорость света равна 1 (т. е. одной световой секунде в секунду). В дальнейшем, как правило, мы будем использовать такие единицы измерения.

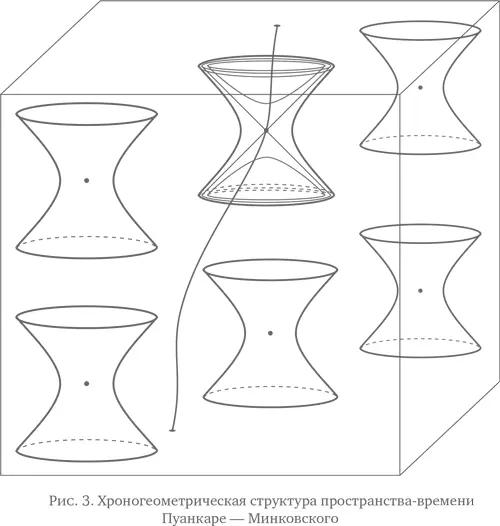
Понятие интервала между двумя событиями определяет то, что можно назвать «хроногеометрией» (или, если угодно, «хроногеометрией») пространства-времени, т. е. обобщение геометрии обычного пространства в том виде, как она определяется понятием расстояния между двумя точками. Геометрию пространства можно представить себе мысленно, изображая вокруг каждой точки P геометрическое место точек, находящихся на единичном расстоянии от точки P, т. е. сферу. Аналогично, хроногеометрию пространства-времени можно изобразить, представив вокруг каждого события P множество событий, разделенных с P единичным квадратом интервала. Однако, поскольку квадрат интервала между двумя событиями может быть положительным, отрицательным или нулевым, мы видим, что полное представление о хроногеометрии пространства-времени будет складываться из определения для каждой точки P форм, соответствующих трем типам событий: (i) события, разделенные с Р квадратом интервала, равным плюс один; (ii) события, разделенные с Р квадратом интервала, равным минус один; и (iii) события, разделенные с Р нулевым интервалом.

Эти множества событий не представляют собой сферы, как в случае евклидовой геометрии. Читатель найдет представление множеств (i), (ii) и (iii) на рис. 3. Заметим, что множество (iii) представляет собой двойной конус, состоящий из двух конусов, соединенных своими вершинами (один конус направлен «в верх» пространства-времени, т. е. к тому, что традиционно называется будущим, тогда как другой конус направлен «в низ» пространства-времени, т. е. к прошлому). Поскольку этот конус представляет собой события, связанные с событием Р посредством светового луча, он называется «световым конусом». Множество (i) имеет форму песочных часов (иными словами, выглядит как два конуса, соединенные своими вершинами, а затем деформированные таким образом, чтобы образовать горловину, через которую может сыпаться песок). Множество (ii) состоит из двух отдельных поверхностей: одна находится в верхней части светового конуса (направленного в будущее), а другая – в нижней его части (направленной в прошлое).

Рисунок 3, на котором представлена хроногеометрия пространства-времени, по своему виду напоминает то, что можно было бы назвать мировой шахматной доской . «Мир» в смысле Минковского означает пространство-время, тогда как структура «шахматной доски» определяет правила, разрешающие ходы между «клетками шахматной доски», т. е. между разными событиями пространства-времени. Например, световой конус указывает на возможность соединения двух событий посредством обмена световым лучом. Интересно также отметить, что шахматная доска состоит из фигур, напоминающих песочные часы. Временной поток отсутствует в пространстве-времени, однако каждые песочные часы напоминают нам о том, что даже в этом мире, существующем вне времени, структуры имеют вид необратимого потока. Возможно, Гераклит, представлявший себе время ребенком, играющим в шахматы {49}, как свидетельствует эпиграф к этой главе, оценил бы такой образ мировой шахматной доски.

Мировая шахматная доска Минковского ничего не содержит. Она представляет собой пространственно-временной фон, который обрамляет существование материи и ее взаимодействия. Чтобы придать наблюдаемое значение хроногеометрии этого мира, необходимо заполнить его объектами, способными почувствовать эту хроногеометрию. Напомним, что, как и в приведенном выше примере мира насекомых на полу, объект, такой как насекомое, имеющий заметную продолжительность жизни, оставляет след в виде трубы, проходящей снизу вверх в пространстве-времени. Жизнь человека также описывается подобной пространственно-временной трубой (рис. 4). Эта труба соответствует ходулям в приведенном выше отрывке из Пруста. Отметим также, что интуиция Пруста не обманула: эта труба занимает место, гораздо более значительное во времени, нежели в пространстве.