Мы видим, что эти два треугольника подобны (то есть они отличаются размерами, но не отношением сторон друг к другу), поскольку оба являются равнобедренными (у них по две одинаковые стороны), и между сторонами одинаковой длины один и тот же небольшой угол Δθ. Поэтому отношения короткой и длинной сторон в обоих треугольниках должны быть взаимно равны. То есть
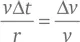
и, значит,
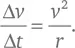
Это – выведенная Гюйгенсом формула центростремительного ускорения.
33. Сравнение Луны с падающим телом
Древние считали, что между явлениями земными и небесными есть принципиальная разница. Ньютон решительно бросил вызов этой точке зрения, сопоставив центростремительное ускорение, которое испытывает Луна при движении по орбите вокруг Земли, с направленным вниз ускорением, которое испытывает тело, падающее вблизи земной поверхности.
Благодаря измерениям суточного параллакса Луны среднее расстояние между Луной и Землей уже было достоверно известно во времена Ньютона – оно составляет 60 радиусов Земли (точное значение равно 60,27). Рассчитывая размер земного радиуса, Ньютон принял, что 1’ (одна минута дуги) на экваторе равна одной миле, или 1024 м, поэтому для полной окружности в 360°, притом что в одном градусе 60’, радиус Земли составил:
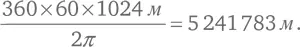
На самом деле средний радиус Земли равен 6 371 000 м – это различие стало наиболее значительным источником ошибки в расчете, выполненном Ньютоном. Орбитальный период Луны (сидерический месяц) был известен точно, он равен 27,3 суток, или 2 360 000 секунд. Значит, орбитальная скорость Луны равна:
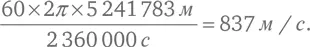
Отсюда центростремительное ускорение Луны равно:
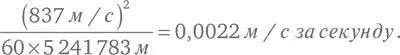
По закону обратных квадратов это число должно было совпасть со значением ускорения свободного падения тел на поверхности Земли, 9,81 м/с за секунду, деленным на квадрат отношения радиуса орбиты Луны к радиусу земного шара:
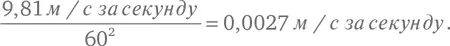
Сравнивая «наблюдаемое» значение центростремительного ускорения Луны (0,0022 м/с за секунду) и расчетное значение, которое он получил из закона обратных квадратов (0,0027 м/с за секунду), Ньютон заявил, что «они достаточно хорошо совпадают» [32]. Впрочем, позже он получил лучший результат.
34. Закон сохранения импульса
Пусть два движущихся объекта с массами m 1и m 2сталкиваются лоб в лоб. Если за некоторый короткий промежуток времени δ t объект 1 воздействует на объект 2 с силой F , то за этот промежуток времени второй объект подвергнется действию ускорения a 2, которое согласно Второму закону механики Ньютона будет удовлетворять равенству m 2 a 2= F . Его скорость v 2 после этого изменится на величину:
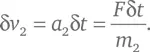
Согласно Третьему закону Ньютона второе тело подействует на первое с силой – F , которая равна по величине, но противоположна по направлению (на что указывает знак «минус»), поэтому в тот же промежуток времени скорость первого объекта v 1изменится в направлении, противоположном δ v 2, на величину:
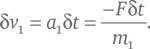
Тогда суммарное изменение общего импульса m 1 v 1 + m 2 v 2 равно:
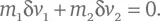
Конечно, два объекта могут оставаться в соприкосновении в течение более продолжительного времени, на протяжении которого сила не остается постоянной, но, так как суммарный импульс сохраняется в каждый малый промежуток времени, он сохраняется и все то время, пока длится столкновение.
В эпоху Ньютона было известно, что четыре тела Солнечной системы обладают спутниками: у Юпитера, Сатурна и Земли есть свои спутники, а все планеты в то же время сами являются спутниками Солнца. По Закону всемирного тяготения тело массой M оказывает воздействие силой F = GMm / r ² на спутник массой m на расстоянии r (где G – мировая гравитационная постоянная), поэтому по Второму закону Ньютона центростремительное ускорение, которое испытывает этот спутник, вычисляется как a = F / m = GM / r ². Значение константы G и общие размеры Солнечной системы еще не были известны во времена Ньютона, но эти неизвестные величины не фигурируют в выражениях для отношений масс, рассчитываемых исходя из отношений расстояний и отношений центростремительных ускорений. Если два спутника тел с массами M 1и M 2обнаруживаются на некоторых расстояниях r 1и r 2от своих центральных тел, для которых известно их отношение r 1/ r 2, а также отношение их центростремительных ускорений a 1/ a 2, то отношение масс двух тел можно найти по формуле:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

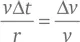
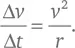
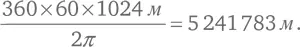
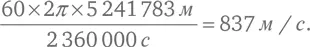
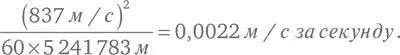
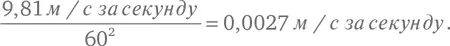
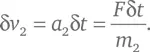
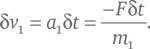
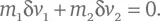






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)



