Игорь Джавадов - Понятная физика

Задача. Предлагаем читателю вычислить энергию поглощения для третьей линии Лаймана (n=1, m=4) и сравнить её с энергией излучения ε = E 4– E 1из данных (47.1).

Для полноты картины рассмотрим спектральную серию III. Чтобы узнать, куда попадают линии этой серии, вычислим для них наибольшую частоту. Она получается из (49.2) при n = 3 и m = ∞. Тогда имеем: ν ∞3=3.29*10 15/9 = 0.363х10 15(Гц). Это соответствует классической длине волны (λ = c/ν): λ ∞3= 2.99х10 8/0.363х10 15= 824 (нм). Известно, что видимый свет занимает диапазон примерно от 400 до 800 (нм). Следовательно, все линии серии III находятся в инфракрасной области, т. е. они невидимы. Серия № 3 носит имя Пашена. Имея инфракрасный спектрометр, можно выявить в этой области также серию Брэкета (n=4), Пфунда (n=5) и другие, представляющие скорее теоретический интерес. Таким образом, из всего спектра атома водорода человек может видеть только несколько фотонов из серии Бальмера (n = 2).

Полученные результаты будут более наглядны, если линии спектра водорода свести в таблицу. Во избежание путаницы, номера энергетических уровней (n, m) в атоме водорода взяты в круглые скобки. Значения энергии квантов поглощения, образующих серии (числа без скобок), посчитаны до серии № 6 (серия Хэмфри).

Таблица 1.Спектр поглощения атома водорода

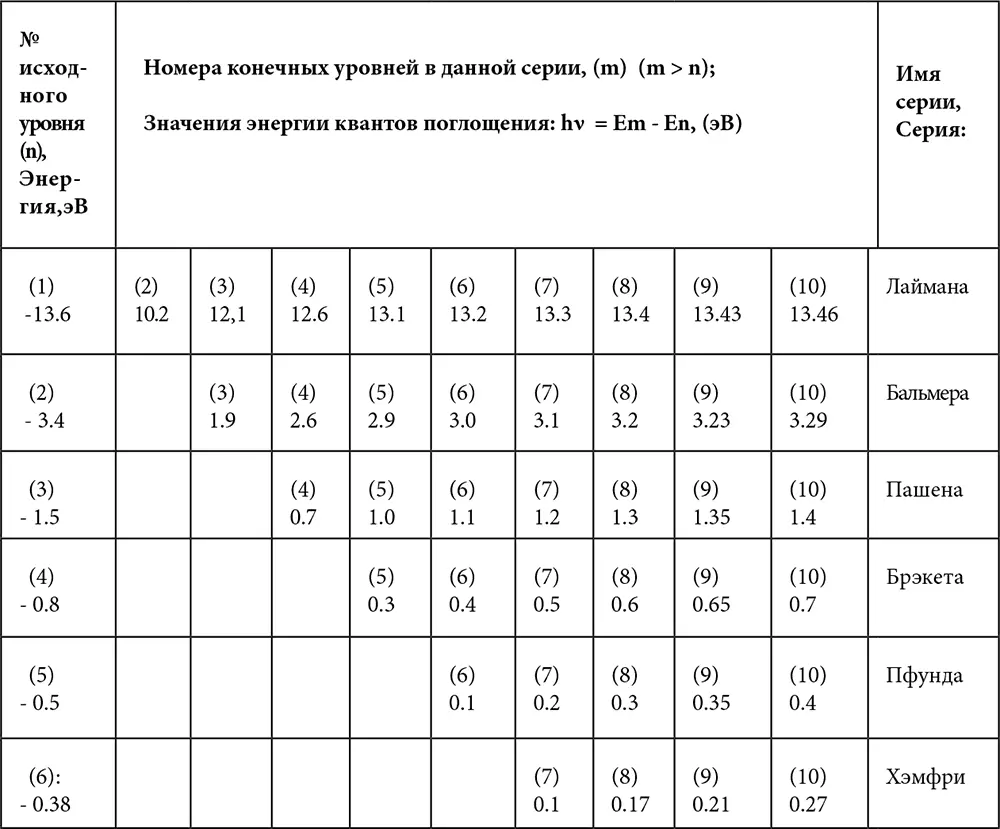
Задача. Предлагается рассчитать по формуле (49.2) серию линий для n=8 (вдруг серию № 7 уже кто-то посчитал). Получится серия № 8, которая будет лежать в очень далекой инфракрасной области (энергия квантов будет составлять сотые доли эВ). Эту серию читатель может назвать своим именем.

Следует заметить, что не все линии поглощения, указанные в таблице 1, можно увидеть даже при помощи спектрометра. Многое зависит от интенсивности – вероятности перехода электрона между конкретными орбитами. Если вероятность перехода мала, например, один-два в месяц, то это слишком мало, чтобы получилась четкая линия Фраунгофера.

Докажем, что теория квантов подтверждается спектральными данными, конкретно, значением постоянной Ридберга. Для этого умножим обе части уравнения (49.2) на h: hν = hR(1/n 2– 1/m 2) = hR/n 2– hR/m 2(50.1). Из теории квантов: hν = E m– E n(50.2). Подставив (50.2) в (50.1), получаем: E m– E n= hR/n 2– hR/m 2(50.3). Уравнение (50.3) будет верно, если E m= – hR/m 2(50.4), и E n= – hR/n 2(50.5). Уравнение (50.5) показывает, что энергия электрона зависит от обратного квадрата номера его орбиты. Подставляя R в (50.5), получаем для первой орбиты (n=1): Е 1=-4.136*10 -15*3.29*10 15= – 13.6 (эВ), что прекрасно совпадает с опытными данными (47.1). Если пойти дальше, то для n = 2: E 2= E 1/4 = -13.6/4 = -3.4 (эВ), для № 3: E 3= -13.6/9 = -1.5, что полностью соответствует (47.1).

Мы доказали, что теория квантов объясняет линейчатость атомных спектров. Классическая теория МаксвеллаГерца не смогла это сделать.

Фотоэффектом называется явление, в котором свет выбивает электроны из вещества. Фотоэффект открыл Герц, когда проводил опыты с искровым разрядником для создания электромагнитных импульсов. В полупроводниках фотоэффект может быть еще и внутренним, когда электроны, выбитые светом из узлов решетки, остаются внутри кристалла, повышая его электропроводность. Очевидно, скорость фотоэлектронов зависит от энергии света. Но что такое – «энергия света»? Следует заметить, что Герц открыл много физических эффектов, большую часть которых объяснить не смог. Ирония судьбы в том, что, доказывая существование электромагнитных волн, Герц нечаянно сделал открытие, которое первым нанесло удар по его волновой теории света. Разберемся по порядку.

Из теории Максвелла-Герца следует, что из двух световых волн с одинаковой частотой волна, имеющая большую амплитуду, переносит больше энергии. Для механических волн это оправдано: чем больше амплитуда волны прибоя, тем дальше на берег она выкинет бутылку с запиской. Из электромагнитной теории света следует, что освещенность пропорциональна амплитуде световой волны. Это значит, чем больше освещенность поверхности образца, тем больше энергии ему передается, тем больше должна быть скорость выбитых фотоэлектронов. В опытах Герца это предположение не подтвердилось.

Столетов доказал, что скорость фотоэлектронов зависит от частоты (цвета) света, а от степени освещенности образца зависит количество фотоэлектронов. Более того, если частоту света плавно уменьшать (цвет смещать в сторону красного), то наступает момент, когда свет не может выбить из вещества ни одного электрона даже при повышенной освещенности. Частоту отсечки фотоэффекта Столетов назвал его красной границей. Существование красной границы фотоэффекта стало для Герца полной неожиданностью. Он так и не смог ее объяснить.