Шон Кэрролл - Частица на краю Вселенной. Как охота на бозон Хиггса ведет нас к границам нового мира

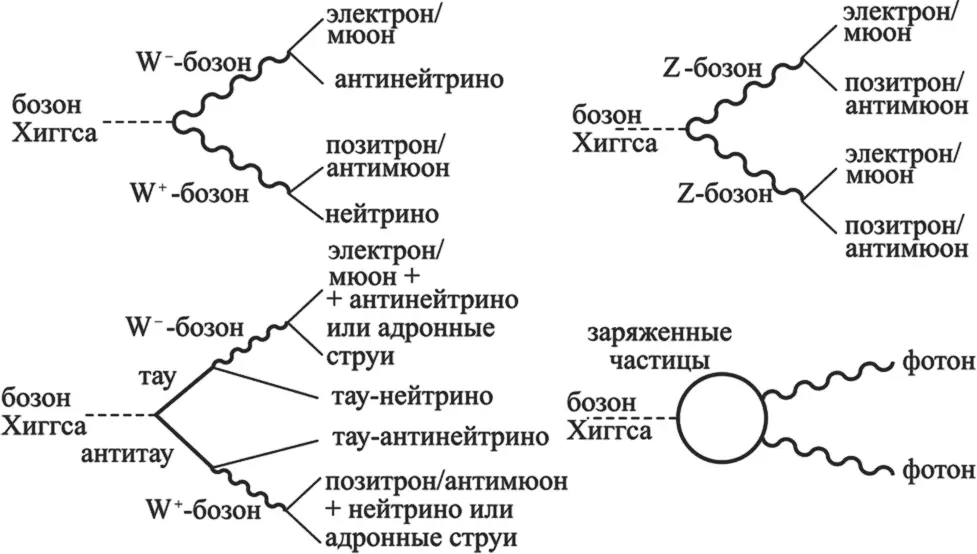
Четыре наиболее перспективных для наблюдений способа распада бозона Хиггса с массой 125 ГэВ. Итак, бозон Хиггса может распасться: 1) на 2 W-бозона, которые затем (иногда) распадаются на электроны или мюоны и соответствующие им нейтрино; 2) на два Z-бозона, которые потом (иногда) могут распасться на электроны или мюоны и их античастицы; 3) на пару тау-антитау, которая потом распадется на два нейтрино и другие фермионы; 4) на некоторую заряженную частицу, которая потом превратится в два фотона. Это все редкие процессы, но они относительно легко обнаруживаются в экспериментах.

Мы сделали краткий тур по различным возможным путям распада бозона Хиггса. Казалось бы, всего лишь поверхностный обзор, но, чтобы получить такие результаты, теоретики затратили огромные усилия, определяя свойства таинственной частицы. Эти исследования начались в 1975 году с опубликования классической работы сотрудников ЦЕРНа Джона Эллиса, Мари К. Гайар и Димитрия Нанопулоса. Они рассмотрели способы, которыми могут быть получены бозоны Хиггса, а также методы их обнаружения. С тех пор было написано множество работ на эту тему, в том числе даже настоящее «Руководство по охоте на бозон Хиггса» (The Higgs Hunter’s Guide) Джона Ганиона, Говарда Хабера, Гордона Кейна и Салли Доусон – книга заняла почетное место на книжных полках у целого поколения физиков, занимающихся элементарными частицами.

Когда все это начиналось, мы мало что знали про бозон Хиггса. Его масса была совершенно произвольным числом, и мы узнали ее только благодаря добросовестным усилиям экспериментаторов. В статье Эллиса, Гайар и Нанопулоса авторы склонялись к тому, что масса бозона равна 10 ГэВ или того меньше и подробно описывали эту область. Если это было бы так, мы давным-давно нашли бы бозон Хиггса, но Природа оказалась к нам не столь добра. Авторы не могли не поддаться искушению и закончили свою статью «извинениями и предостережениями»:

Приносим свои извинения экспериментаторам за то, что не имеем никакого понятия о величине массы бозона Хиггса… и кроме того, уверены, что знаем немного и о его взаимодействиях с другими частицами, разве что они, вероятно, все очень малы. По этим причинам мы не считаем разумным начинать большие эксперименты по поискам бозона Хиггса, но полагаем, что люди, ставящие эксперименты, в которых вероятно появление бозона Хиггса, должны знать, как он может выглядеть.

К счастью, проведение больших экспериментальных исследований было в конечном счете признано разумными, хотя для этого и потребовалось некоторое время. И теперь они окупаются.

Поиск бозона Хиггса часто сравнивают с поисками иголки в стоге сена (или даже иголки в нескольких стогах сена). Дэвид Бриттон – физик из Глазго, который устанавливал грид-систему БАКа в Великобритании, придумал лучшую аналогию: «Это похоже на поиски нужной соломинки в стоге сена. Разница в том, что если вы ищете иголку в стоге сена, то когда и если вы ее найдете, вы узнаете иголку, поскольку она не похожа на сено… а единственный способ найти то, что нам нужно, – разобрать стог, выложить все соломинки в ряд, и если вдруг обнаружится, что какая-то из них имеет определенную длину, это и будет именно то, что мы ищем».

И действительно, есть большая проблема: любой отдельный распад бозона Хиггса, даже на «хорошие» частицы вроде двух фотонов или четырех лептонов, можно принять за другие процессы с тем же исходом, в которых бозон Хиггса никак не замешан (и чаще всего они и происходят). Вы не просто ищете событие данного конкретного типа, вы ищете некоторое увеличение количества событий определенного типа – стог сена, сложенный из соломинок разной длины, в котором вы ищете небольшой избыток соломинок одного определенного размера. Для этого не нужно скрупулезно изучать каждую соломинку – следует обратиться к статистике.

Чтобы лучше понять роль статистики в поисках бозона Хиггса, начнем с более простой задачи. У вас есть монетка, на одной стороне которых изображен орел, на другой – решка, и вы хотите проверить, действительно ли монетка «правильная» – при подбрасывании монеты орел и решка должны выпадать с вероятностью 50 на 50. Проверить справедливость этого утверждения, подбросив монету лишь два или три раза, нельзя – с таким небольшим числом испытаний вы не должны удивляться любому результату. Но чем больше раз вы будете подкидывать монету, тем точнее будет подтверждаться справедливость утверждения о равенстве исходов.