причем

где оператор р^ определяется на языке p -представления уравнением (18.47).
[И опять при желании можно показать, что матричная запись р^ такова:
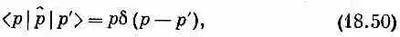
и что

Выводится это так же. как и для х.
Теперь возникает интересный вопрос. Мы можем написать < р > сртак, как мы это сделали в (18.45) и (18.48); смысл оператора р^ в импульсном представлении нам тоже известен. Но как истолковать р^ в координатном представлении? Это бывает нужно знать, если у нас есть волновая функция y ( x )и мы собираемся вычислить ее средний импульс. Позвольте более четко пояснить, что имеется в виду. Если мы начнем с того, что зададим < p > cpуравнением (18.48), то это уравнение можно будет разложить по p -представлению и вернуться к (18.45). Если нам задано p -представление состояния, а именно амплитуда < p |y> как алгебраическая функция импульса p , то из (18.47) можно получить < p |b> и продолжить вычисление интеграла. Вопрос теперь в следующем: а что делать, если нам задано описание состояния в x -представлении, а именно волновая функция y ( x )=< x |y>?
Ну что ж, начнем раскладывать (18.48) в x -представлении.
Напишем
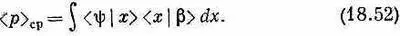
Но теперь надо знать другое: как выглядит состояние |b> в x -представлении. Если мы узнаем это, мы сможем взять интеграл. Итак, наша задача — найти функцию b ( x )=< x |b>. Ее можно найти следующим образом. Мы видели в гл. 14, § 3, как < р |b> связано с < x |b>. Согласно уравнению (14.24),
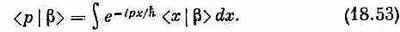
Если нам известно < р |b>, то, решив это уравнение, мы найдем < x |b>. Но результат, конечно, следовало бы как-то выразить через y ( x )=< x |y>, потому что считается, что именно эта величина нам известна. Будем теперь исходить из (18.47) и, опять применив (14.24), напишем
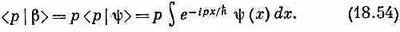
Интеграл берется по х, поэтому р можно внести под интеграл
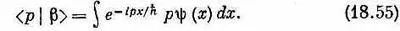
Теперь сравним это с (18.53). Может быть, вы подумали, что < x |b> равно p y( x )? Нет, напрасно! Волновая функция < х |b>=b( x ) может зависеть только от х, но не от р . В этом-то вся трудность.
К счастью, кто-то заметил, что интеграл в (18.55) можно проинтегрировать по частям. Производная e - ipx / h по х равна (-i/h)pe - ipx / h , поэтому интеграл (18.55) это все равно, что
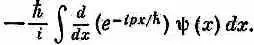
Если это проинтегрировать по частям, оно превратится в
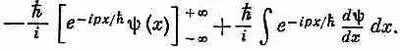
Пока речь идет только о связанных состояниях, y( x ) стремится к нулю при х® ±Ґ, скобка равна нулю и мы имеем
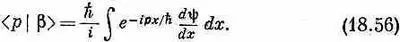
А вот теперь сравним этот результат с (18.53). Вы видите, что

Все необходимое, чтобы взять интеграл в (18.52), у нас уже есть. Окончательный ответ таков:
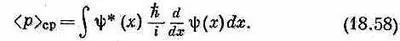
Мы узнали, как выглядит (18.48) в координатном представлении. Перед нами начинает постепенно вырисовываться интересная картина. Когда мы задали вопрос о средней энергии состояния |y>, то ответ был таков:
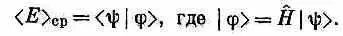
Читать дальше


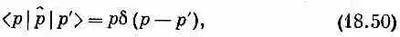

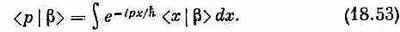
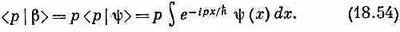
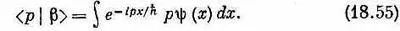
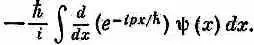
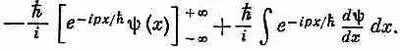
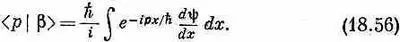

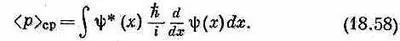
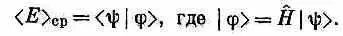



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


